Matter wave
Wave-like behavior of matter has been experimentally demonstrated, first for electrons in 1927 and for other elementary particles, neutral atoms and molecules in the years since.Matter wave concepts are widely used in the study of materials where different wavelength and interaction characteristics of electrons, neutrons, and atoms are leveraged for advanced microscopy and diffraction technologies.In 1900, this division was questioned when, investigating the theory of black-body radiation, Max Planck proposed that the thermal energy of oscillating atoms is divided into discrete portions, or quanta.[1] Extending Planck's investigation in several ways, including its connection with the photoelectric effect, Albert Einstein proposed in 1905 that light is also propagated and absorbed in quanta,[2]: 87 now called photons.Einstein's postulate was verified experimentally[2]: 89 by K. T. Compton and O. W. Richardson[4] and by A. L. Hughes[5] in 1912 then more carefully including a measurement of the Planck constant in 1916 by Robert Millikan.[6] When I conceived the first basic ideas of wave mechanics in 1923–1924, I was guided by the aim to perform a real physical synthesis, valid for all particles, of the coexistence of the wave and of the corpuscular aspects that Einstein had introduced for photons in his theory of light quanta in 1905.De Broglie, in his 1924 PhD thesis,[8] proposed that just as light has both wave-like and particle-like properties, electrons also have wave-like properties.His thesis started from the hypothesis, "that to each portion of energy with a proper mass m0 one may associate a periodic phenomenon of the frequency ν0, such that one finds: hν0 = m0c2.then integrating, de Broglie arrived at his formula for the relationship between the wavelength, λ, associated with an electron and the modulus of its momentum, p, through the Planck constant, h:[14]Inspired by Debye's remark, Erwin Schrödinger decided to find a proper three-dimensional wave equation for the electron.The Schrödinger equation describes the time evolution of a wavefunction, a function that assigns a complex number to each point in space.The de Broglie hypothesis and the existence of matter waves has been confirmed for other elementary particles, neutral atoms and even molecules have been shown to be wave-like.Recently, a close copy of the famous double-slit experiment[27]: 260 using electrons through physical apertures gave the movie shown.[28] In 1927 at Bell Labs, Clinton Davisson and Lester Germer fired slow-moving electrons at a crystalline nickel target.At the same time George Paget Thomson and Alexander Reid at the University of Aberdeen were independently firing electrons at thin celluloid foils and later metal films, observing rings which can be similarly interpreted.[21] (Alexander Reid, who was Thomson's graduate student, performed the first experiments but he died soon after in a motorcycle accident[29] and is rarely mentioned.)[30] The matter wave interpretation was placed onto a solid foundation in 1928 by Hans Bethe,[31] who solved the Schrödinger equation,[16] showing how this could explain the experimental results.Neutrons, produced in nuclear reactors with kinetic energy of around 1 MeV, thermalize to around 0.025 eV as they scatter from light atoms.The resulting de Broglie wavelength (around 180 pm) matches interatomic spacing and neutrons scatter strongly from hydrogen atoms.[35] In 1944, Ernest O. Wollan, with a background in X-ray scattering from his PhD work[36] under Arthur Compton, recognized the potential for applying thermal neutrons from the newly operational X-10 nuclear reactor to crystallography.[39] Interference of atom matter waves was first observed by Immanuel Estermann and Otto Stern in 1930, when a Na beam was diffracted off a surface of NaCl.[43] Recent experiments confirm the relations for molecules and even macromolecules that otherwise might be supposed too large to undergo quantum mechanical effects.Examples include: The third class are matter waves which have a wavevector, a wavelength and vary with time, but have a zero group velocity or probability flux.By contrast, strongly interacting particles like slow electrons and molecules require vacuum: the matter wave properties rapidly fade when they are exposed to even low pressures of gas.Electron optical systems use stabilized high voltage to give a narrow energy spread in combination with collimating (parallelizing) lenses and pointed filament sources to achieve good coherence."[72] Laser light momentum transfer can cool matter particles and alter the internal excitation state of atoms.[74] The following subsections provide links to pages describing applications of matter waves as probes of materials or of fundamental quantum properties.Unlike light, matter wave particles may have mass, electric charge, magnetic moments, and internal structure, presenting new challenges and opportunities.Beams of electrons also lead to characteristic X-rays in energy dispersive spectroscopy which can produce information about chemical content at the nanoscale.Small-angle neutron scattering provides way to obtain structure of disordered systems that is sensitivity to light elements, isotopes and magnetic moments.[83][84] Matter-wave interfererometers generate nanostructures on molecular beams that can be read with nanometer accuracy and therefore be used for highly sensitive force measurements, from which one can deduce a plethora or properties of individualized complex molecules.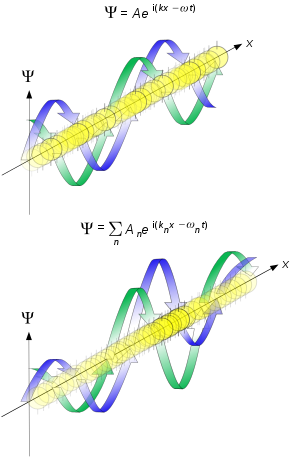


Mechanical waveQuantum mechanicsSchrödinger equationIntroductionGlossaryHistoryClassical mechanicsOld quantum theoryBra–ket notationHamiltonianInterferenceComplementarityDecoherenceEntanglementEnergy levelMeasurementNonlocalityQuantum numberSuperpositionSymmetryTunnellingUncertaintyWave functionCollapseBell's inequalityCHSH inequalityDavisson–GermerDouble-slitElitzur–VaidmanFranck–HertzLeggett inequalityLeggett–Garg inequalityMach–ZehnderPopperQuantum eraserDelayed-choiceSchrödinger's catStern–GerlachWheeler's delayed-choiceOverviewHeisenbergInteractionMatrixPhase-spaceSchrödingerSum-over-histories (path integral)Klein–GordonRydbergInterpretationsBayesianConsistent historiesCopenhagende Broglie–BohmEnsembleHidden-variableSuperdeterminismMany-worldsObjective-collapseQuantum logicRelationalTransactionalVon Neumann–WignerRelativistic quantum mechanicsQuantum field theoryQuantum information scienceQuantum computingQuantum chaosEPR paradoxDensity matrixScattering theoryQuantum statistical mechanicsQuantum machine learningAharonovBlackettde BroglieComptonDavissonEhrenfestEinsteinEverettFeynmanGlauberGutzwillerHilbertJordanKramersLandauMoseleyMillikanPlanckSimmonsSommerfeldvon NeumannWignerZeemanZeilingerwave–particle dualitymatterelectronsdiffractedLouis de BrogliewavelengthmomentumPlanck constantelementary particlesmoleculesMaxwell's equationsblack-body radiationMax Planckphotoelectric effectAlbert EinsteinphotonsPlanck–Einstein relationGreek letter nuGreek letter lambdafrequencyK. T. ComptonO. W. RichardsonRobert Millikancomplexopacityplane wavewave packetproper massCompton frequencyspecial relativity