Quantum complexity theory
For instance, the complexity class P is defined as the set of problems solvable by a Turing machine in polynomial time.In short the modern Church-Turing thesis states that any computational model can be simulated in polynomial time with a probabilistic Turing machine.[1][2] However, questions around the Church-Turing thesis arise in the context of quantum computing.It is unclear whether the Church-Turing thesis holds for the quantum computation model.It may not be possible for a probabilistic Turing machine to simulate quantum computation models in polynomial time.The important complexity classes P, BPP, BQP, PP, and PSPACE can be compared based on promise problems.[4] The class of problems that can be efficiently solved by a quantum computer with bounded error is called BQP ("bounded error, quantum, polynomial time").More formally, BQP is the class of problems that can be solved by a polynomial-time quantum Turing machine with error probability of at most 1/3.; that is, the class of problems that can be efficiently solved by quantum computers includes all problems that can be efficiently solved by deterministic classical computers but does not include any problems that cannot be solved by classical computers with polynomial space resources.It is further suspected that BQP is a strict superset of P, meaning there are problems that are efficiently solvable by quantum computers that are not efficiently solvable by deterministic classical computers.For instance, integer factorization and the discrete logarithm problem are known to be in BQP and are suspected to be outside of P. On the relationship of BQP to NP, little is known beyond the fact that some NP problems are in BQP (integer factorization and the discrete logarithm problem are both in NP, for example).[3] This number of classical gates is obtained by determining how many bit operations are necessary to simulate the quantum circuit.dimensions and entries that are the amplitudes associated with each basis state or component vector.[9] In order to obtain an upper bound for the number of gates required to simulate a quantum circuit we need a sufficient upper bound for the amount data used to specify the information about each of thebit operations for every quantum gate applied to the state vector.[4] One major advantage of using a quantum computational system instead of a classical one, is that a quantum computer may be able to give a polynomial time algorithm for some problem for which no classical polynomial time algorithm exists, but more importantly, a quantum computer may significantly decrease the calculation time for a problem that a classical computer can already solve efficiently.[10] When considering quantum computation of the solution to directed graph problems, there are two important query models to understand.Additionally, the adjacency array model satisfies the simple graph condition,[11] Both of the above models can be used to determine the query complexity of particular types of graphing problems, including the connectivity, strong connectivity (a directed graph version of the connectivity model), minimum spanning tree, and single source shortest path models of graphs.An important caveat to consider is that the quantum complexity of a particular type of graphing problem can change based on the query model (namely either matrix or array) used to determine the solution.The following table showing the quantum query complexities of these types of graphing problems illustrates this point well.In the query complexity model, the input can also be given as an oracle (black box).Similar to the case of graphing problems, the quantum query complexity of a black-box problem is the smallest number of queries to the oracle that are required in order to calculate the function.An example depicting the power of quantum computing is Grover's algorithm for searching unstructured databases.A classical deterministic algorithm will have to check more than half of the possible inputs to be sure of whether or not the function is constant or balanced.possible inputs, the query complexity of the most efficient classical deterministic algorithm is[2] The Deutsch-Jozsa algorithm takes advantage of quantum parallelism to check all of the elements of the domain at once and only needs to query the oracle once, making its query complexityFor instance, it has been shown that a non-local hidden variable quantum computer based on Bohmian Mechanics could implement a search of an N-item database in at mostNote, however, that neither search method would allow quantum computers to solve NP-complete problems in polynomial time.However, defining computation in these theories is an open problem due to the problem of time; that is, within these physical theories there is currently no obvious way to describe what it means for an observer to submit input to a computer at one point in time and then receive output at a later point in time.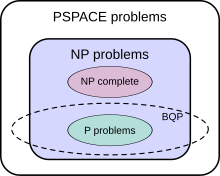
computational complexity theorycomplexity classesquantum computerscomputational modelquantum mechanicscomputational problemsComputational complexityComplexity classTuring machinepolynomial timequantum circuit modelquantum Turing machinePSPACEChurch-Turing thesisprobabilistic Turing machineasymptotic notationBig O notationpromise problemsproblemsprobabilistic Turing machinesinteger factorizationdiscrete logarithm problemNP-completeNP-hardness
#
P
{\displaystyle \color {Blue}{\mathsf {\#P}}}
quantum circuitclassical gateslinear combinationcomponent vectorsDirac notationsparse matricespolynomial time algorithmdirected graphsadjacency matrixadjacency listsSpanning treeconnectivitystrong connectivityminimum spanning treesingle source shortest pathGrover's algorithmlinear searchasymptotically optimalDeutsch-Jozsa algorithmblack boxoracledeterministic algorithmBohmian Mechanicsquantum gravityM-theoryloop quantum gravityproblem of timeQuantum computingPolynomial hierarchyBibcodeNielsen, MichaelChuang, IsaacCiteSeerXAaronson, ScottQuantum Computation and Quantum InformationArora, SanjeevBarak, BoazWatrous, JohnScott AaronsonQuantum information scienceDiVincenzo's criteriaNISQ eratimelineQuantum informationQuantum programmingQuantum simulationphysical vs. logicalQuantum processorscloud-basedBell'sEastin–KnillGleason'sGottesman–KnillHolevo'sNo-broadcastingNo-cloningNo-communicationNo-deletingNo-hidingNo-teleportationQuantum speed limitThresholdSolovay–KitaevPurificationClassical capacityentanglement-assistedquantum capacityEntanglement distillationMonogamy of entanglementQuantum channelquantum networkQuantum teleportationquantum gate teleportationSuperdense codingQuantum cryptographyPost-quantum cryptographyQuantum coin flippingQuantum moneyQuantum key distributionSARG04other protocolsQuantum secret sharingQuantum algorithmsAmplitude amplificationBernstein–VaziraniBoson samplingDeutsch–JozsaGrover'sHidden subgroupQuantum annealingQuantum countingQuantum Fourier transformQuantum optimizationQuantum phase estimationShor'sSimon'sPostBQPQuantum supremacyQuantum volumeRandomized benchmarkingRelaxation times