Complexity class
In particular, most complexity classes consist of decision problems that are solvable with a Turing machine, and are differentiated by their time or space (memory) requirements.For instance, the class P is the set of decision problems solvable by a deterministic Turing machine in polynomial time.The study of the relationships between complexity classes is a major area of research in theoretical computer science.In particular, most complexity classes consist of decision problems that can be solved by a Turing machine with bounded time or space resources.For example, the complexity class P is defined as the set of decision problems that can be solved by a deterministic Turing machine in polynomial time.Mechanically, a Turing machine (TM) manipulates symbols (generally restricted to the bits 0 and 1 to provide an intuitive connection to real-life computers) contained on an infinitely long strip of tape.from above is the set of strings (representing natural numbers) that a Turing machine running an algorithm that correctly tests for primality accepts.The time complexity of a TM on a particular input is the number of elementary steps that the Turing machine takes to reach either an accept or reject state.In this way, an NTM can be thought of as simultaneously exploring all computational possibilities in parallel and selecting an accepting branch.To do this, computational problems are differentiated by upper bounds on the maximum amount of resources that the most efficient algorithm takes to solve them.More specifically, complexity classes are concerned with the rate of growth in the resources required to solve particular computational problems as the input size increases.Using big O notation, they are defined as follows: P is the class of problems that are solvable by a deterministic Turing machine in polynomial time and NP is the class of problems that are solvable by a nondeterministic Turing machine in polynomial time.That is, a language is in NP if there exists a deterministic polynomial time Turing machine, referred to as the verifier, that takes as input a stringFurthermore, it also provides a useful method for proving that a language is in NP—simply identify a suitable certificate and show that it can be verified in polynomial time.(intuitively, deterministic Turing machines are just a subclass of nondeterministic Turing machines that don't make use of their nondeterminism; or under the verifier definition, P is the class of problems whose polynomial time verifiers need only receive the empty string as their certificate), it is not known whether NP is strictly larger than P. If P=NP, then it follows that nondeterminism provides no additional computational power over determinism with regards to the ability to quickly find a solution to a problem; that is, being able to explore all possible branches of computation provides at most a polynomial speedup over being able to explore only a single branch.[8] EXPTIME (sometimes shortened to EXP) is the class of decision problems solvable by a deterministic Turing machine in exponential time and NEXPTIME (sometimes shortened to NEXP) is the class of decision problems solvable by a nondeterministic Turing machine in exponential time.L (sometimes lengthened to LOGSPACE) is then defined as the class of problems solvable in logarithmic space on a deterministic Turing machine and NL (sometimes lengthened to NLOGSPACE) is the class of problems solvable in logarithmic space on a nondeterministic Turing machine.co-NP, for instance, is one important complement complexity class, and sits at the center of the unsolved problem over whether co-NP=NP.The hierarchy theorems enable one to make quantitative statements about how much more additional time or space is needed in order to increase the number of problems that can be solved.A probabilistic Turing machine is similar to a deterministic Turing machine, except rather than following a single transition function (a set of rules for how to proceed at each step of the computation) it probabilistically selects between multiple transition functions at each step.The randomness introduced at each step of the computation introduces the potential for error; that is, strings that the Turing machine is meant to accept may on some occasions be rejected and strings that the Turing machine is meant to reject may on some occasions be accepted.As a result, the complexity classes based on the probabilistic Turing machine are defined in large part around the amount of error that is allowed.if: The fundamental randomized time complexity classes are ZPP, RP, co-RP, BPP, and PP.Taken together, the classes RP and co-RP encompass all of the problems that can be solved by probabilistic Turing machines with one-sided error.Interactive proof systems are abstract machines that model computation as the exchange of messages between two parties: a proverThe class NC is the set of languages that can be solved by circuit families that are restricted not only to having polynomial-size but also to having polylogarithmic depth.[23] More specifically, FP is the set of function problems that can be solved by a deterministic Turing machine in polynomial time.Formulating many basic complexity classes like P as promise problems provides little additional insight into their nature.Promise problems have, for instance, played a key role in the study of SZK (statistical zero-knowledge).Technically, the breakdown into decidable and undecidable pertains more to the study of computability theory, but is useful for putting the complexity classes in perspective.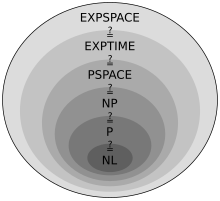





computational complexity theorycomputational problemscomplexitymemorymodel of computationdecision problemsTuring machinepolynomial timecounting problemsfunction problemsprobabilistic Turing machinesinteractive proof systemsBoolean circuitsquantum computerstheoretical computer sciencePSPACEEXPTIMENEXPTIMEEXPSPACEsubsetopen problemsP equals NPnondeterminismdeterministic Turing machinecomputational problemalgorithmnatural numberstringsbinary numbersformal languageslinguisticsdecision problemyes–no questionstests for primalityOptimization problemsPromise problemscomputational modelprocessorBlum axiomsChurch–Turing thesisdeterministicdecidabilityrecognizabilitytime complexityspace complexityNondeterministic Turing machineupper boundspolynomiallogarithmic functionexponential functionList of complexity classesbig O notationP (complexity)NP (complexity)certificateP versus NPL (complexity)NL (complexity)logarithmictwo-tape Turing machinecomputabilityPSPACE (complexity)Savitch's theorem Savitch's theoremclosurenegationdisjunctionconjunctionBoolean operationsReduction (complexity)Cook reductionsKarp reductionsLevin reductionspolynomial-time reductionslog-space reductionsNP-hardcompleteNP-completeTime hierarchy theoremSpace hierarchy theoremTuring machinesP/polyquantum Turing machinesRandomized computationprobabilistic Turing machinerandomized algorithmsquantum complexityone-sided errortwo-sided errorInteractive proof systemcryptographyapproximation algorithmsformal verificationabstract machinesprobabilistic algorithmsCircuit complexityAND gatesOR gatesNOT gatesBoolean circuitdigital circuitscomputersdirected acyclic graphlogic gatesBoolean functionLanguages
P
⊂
P/poly
{\displaystyle {\mathsf {\color {Blue}P}}\subset {\textsf {P/poly}}}
undecidable problemspolynomial hierarchyadvice functiondirected pathparallel algorithmsquantum information scienceCounting problem (complexity)simple cyclefunctionsstatistical estimationstatistical physicsnetwork designeconomicsFunction problemfunctionalphabetPromise problemformal languageplanar graph







