Quantum computing
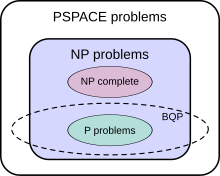
On small scales, physical matter exhibits properties of both particles and waves, and quantum computing leverages this behavior using specialized hardware.Theoretically a large-scale quantum computer could break some widely used encryption schemes and aid physicists in performing physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications.If a quantum computer manipulates the qubit in a particular way, wave interference effects can amplify the desired measurement results.National governments have invested heavily in experimental research that aims to develop scalable qubits with longer coherence times and lower error rates.[17] Peter Shor built on these results with his 1994 algorithm for breaking the widely used RSA and Diffie–Hellman encryption protocols,[18] which drew significant attention to the field of quantum computing.[23] In 1998, a two-qubit quantum computer demonstrated the feasibility of the technology,[24][25] and subsequent experiments have increased the number of qubits and reduced error rates.While programmers may depend on probability theory when designing a randomized algorithm, quantum mechanical notions like superposition and interference are largely irrelevant for program analysis.This can be achieved by preparing a quantum system in a superposition of input states and applying a unitary transformation that encodes the function to be evaluated.The threshold theorem shows how increasing the number of qubits can mitigate errors,[45] yet fully fault-tolerant quantum computing remains "a rather distant dream".[47][48] The Harvard research team was supported by MIT, QuEra Computing, Caltech, and Princeton University and funded by DARPA's Optimization with Noisy Intermediate-Scale Quantum devices (ONISQ) program.Post-quantum cryptography, which involves the development of cryptographic algorithms that are resistant to attacks by both classical and quantum computers, is an active area of research aimed at addressing this concern.Advances in these fields, such as the development of new QKD protocols, the improvement of QRNGs, and the standardization of post-quantum cryptographic algorithms, will play a key role in maintaining the integrity and confidentiality of information in the quantum era.[69] This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem.In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm.Identifying cryptographic systems that may be secure against quantum algorithms is an actively researched topic under the field of post-quantum cryptography.The most well-known example of a problem that allows for a polynomial quantum speedup is unstructured search, which involves finding a marked item out of a list ofIn this case, the advantage is not only provable but also optimal: it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups.[46][82] For example, the HHL Algorithm, named after its discoverers Harrow, Hassidim, and Lloyd, is believed to provide speedup over classical counterparts.[46][83] Some research groups have recently explored the use of quantum annealing hardware for training Boltzmann machines and deep neural networks.However, the immense size and complexity of the structural space of all possible drug-like molecules pose significant obstacles, which could be overcome in the future by quantum computers.Examples include the quantum gates, and the lattice vibrations and background thermonuclear spin of the physical system used to implement the qubits.[95] Currently, some quantum computers require their qubits to be cooled to 20 millikelvin (usually using a dilution refrigerator[96]) in order to prevent significant decoherence.[98] As a result, time-consuming tasks may render some quantum algorithms inoperable, as attempting to maintain the state of qubits for a long enough duration will eventually corrupt the superpositions.Careful estimates[101][102] show that at least 3 million physical qubits would factor 2,048-bit integer in 5 months on a fully error-corrected trapped-ion quantum computer.In terms of the number of physical qubits, to date, this remains the lowest estimate[103] for practically useful integer factorization problem sizing 1,024-bit or larger.Another approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads, and relying on braid theory to form stable logic gates.[89][125] In January 2024, a study published in Physical Review Letters provided direct verification of quantum supremacy experiments by computing exact amplitudes for experimentally generated bitstrings using a new-generation Sunway supercomputer, demonstrating a significant leap in simulation capability built on a multiple-amplitude tensor network contraction algorithm.It argues that the most promising candidates for achieving speedup with quantum computers are "small-data problems", for example in chemistry and materials science.However, the article also concludes that a large range of the potential applications it considered, such as machine learning, "will not achieve quantum advantage with current quantum algorithms in the foreseeable future", and it identified I/O constraints that make speedup unlikely for "big data problems, unstructured linear systems, and database search based on Grover's algorithm".Some researchers have expressed skepticism that scalable quantum computers could ever be built, typically because of the issue of maintaining coherence at large scales, but also for other reasons.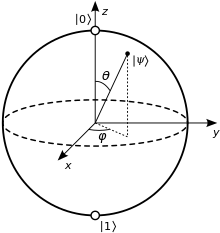



Bloch spherecomputerquantum mechanicalboth particles and wavesClassical physicsexponentiallybreak some widely used encryption schemesphysical simulationsunit of informationbinarysuperpositionmeasuringprobabilistic outputwave interferencequantum algorithmsisolatedquantum decoherencesuperconductorselectrical currentelectrical resistanceion trapsatomic particleelectromagnetic fieldstime complexitycomputabilityquantum complexity theoryquantum supremacyTimeline of quantum computing and communicationquantum mechanicscomputer scienceModern quantum theorydigital computershuman computersWorld War IIwartime cryptographynuclear physicsManhattan ProjectphysicistsqubitsPaul Benioffquantum Turing machineexponentialsimulating quantum dynamicsYuri ManinRichard FeynmanCharles BennettGilles Brassardcryptographyinformation securityoracle problemsDeutsch's algorithmBernstein–Vazirani algorithmSimon's algorithmblack boxPeter ShorRSA encryptionhis 1994 algorithmDiffie–HellmanGrover's algorithmunstructuredSeth Lloydexperimentaliststrapped ionsGoogle AIIntroduction to quantum mechanicsComputer engineersmodern computerclassical electrodynamicssemiconductorsrandom number generatorsquantum informationdecoheresprogrammersprobability theoryrandomized algorithminterferenceprogram analysisQuantum programscoherentdescribe these systems mathematicallylinear algebraComplex numbersprobability amplitudesvectorsquantum statesmatricescomposingCharlie Bennettvector spacevectorDirac notationquantum state vectorprobability vectormeasuredstandard basisBorn rulenorm-squaredcollapsesdimensionstate spacetensor productBell stateentangledUnitarity (physics)quantum memoryquantum logic gatesclassical logic gatesmatrixmatrix multiplicationcontrolled NOT (CNOT)measurement can be deferredquantum circuitsQuantum programmingmodels of computationToffoli gatemore primitive gatesquantum gate arrayquantum gatesunitary matrixuniversal quantum computerSolovay-Kitaev theoremmeasurement-based quantum computercluster statequantum gate teleportationadiabatic quantum computerquantum annealing



