Laplace–Runge–Lenz vector

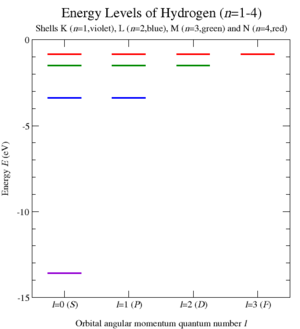
[3][4][5][6] The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force.The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom,[7][8] before the development of the Schrödinger equation.[2][14][16] Various generalizations of the LRL vector have been defined, which incorporate the effects of special relativity, electromagnetic fields and even different types of central forces.can be defined for all central forces, but this generalized vector is a complicated function of position, and usually not expressible in closed form.[15] Jakob Hermann was the first to show that A is conserved for a special case of the inverse-square central force,[22] and worked out its connection to the eccentricity of the orbital ellipse.[23] At the end of the century, Pierre-Simon de Laplace rediscovered the conservation of A, deriving it analytically, rather than geometrically.[25] Gibbs' derivation was used as an example by Carl Runge in a popular German textbook on vectors,[26] which was referenced by Wilhelm Lenz in his paper on the (old) quantum mechanical treatment of the hydrogen atom.This definition of the LRL vector A pertains to a single point particle of mass m moving under the action of a fixed force.[33] Nevertheless, equivalently, they are also quantized in the Nambu framework, such as this classical Kepler problem into the quantum hydrogen atom.The perturbation potential h(r) may be any sort of function, but should be significantly weaker than the main inverse-square force between the two bodies.This approach was used to help verify Einstein's theory of general relativity, which adds a small effective inverse-cubic perturbation to the normal Newtonian gravitational potential,[35]to express r in terms of θ, the precession rate of the periapsis caused by this non-Newtonian perturbation is calculated to be[35]where i=1,2,3 and εijs is the fully antisymmetric tensor, i.e., the Levi-Civita symbol; the summation index s is used here to avoid confusion with the force parameter k defined above.Importantly, by dint of the vanishing of C2, they are independent of the ℓ and m quantum numbers, making the energy levels degenerate.The additional symmetry operators A have connected the different ℓ multiplets among themselves, for a given energy (and C1), dictating n2 states at each level.[51] Classically, the higher symmetry of the Kepler problem allows for continuous alterations of the orbits that preserve energy but not angular momentum; expressed another way, orbits of the same energy but different angular momentum (eccentricity) can be transformed continuously into one another.For negative energies – i.e., for bound systems – the higher symmetry group is SO(4), which preserves the length of four-dimensional vectors[10] Specifically, Fock showed that the Schrödinger wavefunction in the momentum space for the Kepler problem was the stereographic projection of the spherical harmonics on the sphere.Rotation of the sphere and re-projection results in a continuous mapping of the elliptical orbits without changing the energy, an SO(4) symmetry sometimes known as Fock symmetry;[52] quantum mechanically, this corresponds to a mixing of all orbitals of the same energy quantum number n. Valentine Bargmann noted subsequently that the Poisson brackets for the angular momentum vector L and the scaled LRL vector A formed the Lie algebra for SO(4).[11][42] Simply put, the six quantities A and L correspond to the six conserved angular momenta in four dimensions, associated with the six possible simple rotations in that space (there are six ways of choosing two axes from four).For positive energies – i.e., for unbound, "scattered" systems – the higher symmetry group is SO(3,1), which preserves the Minkowski length of 4-vectorsBoth the negative- and positive-energy cases were considered by Fock[10] and Bargmann[11] and have been reviewed encyclopedically by Bander and Itzykson.An elegant action-angle variables solution for the Kepler problem can be obtained by eliminating the redundant four-dimensional coordinatesThe following are arguments showing that the LRL vector is conserved under central forces that obey an inverse-square law.Subtraction and re-expression in terms of the Cartesian momenta px and py shows that Γ is equivalent to the LRL vectorThe connection between the rotational symmetry described above and the conservation of the LRL vector can be made quantitative by way of Noether's theorem.This theorem, which is used for finding constants of motion, states that any infinitesimal variation of the generalized coordinates of a physical systemwhere i equals 1, 2 and 3, with xi and pi being the i-th components of the position and momentum vectors r and p, respectively; as usual, δis represents the Kronecker delta.Noether's theorem derivation of the conservation of the LRL vector A is elegant, but has one drawback: the coordinate variation δxi involves not only the position r, but also the momentum p or, equivalently, the velocity v.[62] This drawback may be eliminated by instead deriving the conservation of A using an approach pioneered by Sophus Lie.[63][64] Specifically, one may define a Lie transformation[51] in which the coordinates r and the time t are scaled by different powers of a parameter λ (Figure 9),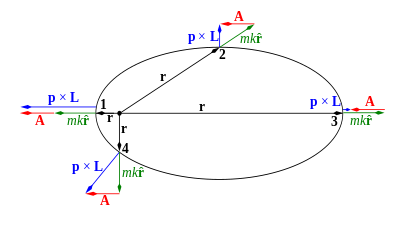
Figure 1: The LRL vector A (shown in red) at four points (labeled 1, 2, 3 and 4) on the elliptical orbit of a bound point particle moving under an inverse-square central force. The center of attraction is shown as a small black circle from which the position vectors (likewise black) emanate. The angular momentum vector L is perpendicular to the orbit. The coplanar vectors p × L and ( mk / r ) r are shown in blue and green, respectively; these variables are defined below . The vector A is constant in direction and magnitude.
Figure 2: Simplified version of Figure 1, defining the angle θ between A and r at one point of the orbit.
Figure 3: The momentum vector p (shown in blue) moves on a circle as the particle moves on an ellipse. The four labeled points correspond to those in Figure 1. The circle is centered on the y -axis at position A / L (shown in magenta), with radius mk / L (shown in green). The angle η determines the eccentricity e of the elliptical orbit ( cos η = e ). By the inscribed angle theorem for circles , η is also the angle between any point on the circle and the two points of intersection with the p x axis, p x = ± p 0 , which only depend on E , but not L .
Figure 5: Gradually precessing elliptical orbit, with an eccentricity e = 0.667. Such precession arises in the Kepler problem if the attractive central force deviates slightly from an inverse-square law. The rate of precession can be calculated using the formulae in the text.
Figure 6: Energy levels of the hydrogen atom as predicted from the commutation relations of angular momentum and Laplace–Runge–Lenz vector operators; these energy levels have been verified experimentally.
Figure 7: The family of circular momentum hodographs for a given energy E . All the circles pass through the same two points on the p x axis (see Figure 3). This family of hodographs corresponds to one family of Apollonian circles , and the σ isosurfaces of bipolar coordinates .
Figure 8: The momentum hodographs of Figure 7 correspond to stereographic projections of great circles on the three-dimensional η unit sphere. All of the great circles intersect the η x axis, which is perpendicular to the page; the projection is from the North pole (the w unit vector) to the η x − η y plane, as shown here for the magenta hodograph by the dashed black lines. The great circle at a latitude α corresponds to an eccentricity e = sin α . The colors of the great circles shown here correspond to their matching hodographs in Figure 7.
Figure 9: The Lie transformation from which the conservation of the LRL vector A is derived. As the scaling parameter λ varies, the energy and angular momentum changes, but the eccentricity e and the magnitude and direction of A do not.
Figure 4: The angular momentum vector L , the LRL vector A and Hamilton's vector, the binormal B , are mutually perpendicular; A and B point along the major and minor axes, respectively, of an elliptical orbit of the Kepler problem.
classical mechanicsvectorbinary startwo bodies interactingNewtonian gravityconstant of motionconservedcentral forceinverse squareKepler problemshydrogen atomCoulomb's lawelectrostaticsquantum mechanicalspectrumSchrödinger equationthe surface of a four-dimensional (hyper-)spherecircleenergyPierre-Simon de LaplaceCarl RungeWilhelm Lenznone of those scientistseccentricity vectorcelestial mechanicsspecial relativityelectromagnetic fieldsconservativeCartesian componentsangular momentummomentumvelocitydot productperiapsiscentral forcesexpressible in closed formcyclic coordinateLagrangianPoisson bracketsJakob HermannellipseJohann BernoulliWilliam Rowan HamiltonJosiah Willard Gibbsvector analysisGermanWolfgang Paulimatrix mechanicspotential energyunit vectorSI unitstwo-body problemsreduced massdimensionlessscalar triple producteccentricityhyperbolaparabolainscribed angle theoremcircleshodographconstants of motionmaximally superintegrableHamilton–Jacobi equationcoordinate systemspherical coordinatesparabolic coordinatesphase spaceisosurfacesNambu mechanicsHamiltonian mechanicsquantizedcommutation relationsapsidal precessionaction-angle coordinatesEinstein'sgeneral relativityMercurypulsarsantisymmetric tensorLevi-Civita symbolLie bracketsnegativepositiveCasimir invariantshydrogen-like atomsoperatorsCasimir operatorenergy levelsladder operatorsHamiltonianidentity operatoreigenstatesenergy levels degenerateRydberg formulaelectronic orbitalsrotation group SO(3)spherical harmonicsquantum numberApollonian circlesbipolar coordinateshigher-dimensional spaceVladimir Fockthree-dimensional unit spherewavefunctionstereographic projectionValentine BargmannuniverseSO(3,1)Minkowski length4-vectorsreflectionO(3,1)connectedsubgroupsgreat circlesaction-angle variablesJacobi's elliptic functionschargeLorentz factordyadic tensorLagrange's formulaBertrand's theoremmultivalued functionNoether's theoremgeneralized coordinatesKronecker deltaSophus LieKepler's third lawbinormaltensor productvector cross productprincipal axestensoreigenvectorsAstrodynamicsOrbital elementsBinet equationTwo-body problemGoldstein, H.Taff, L. G.Arnold, V. I.Sommerfeld, A.Lanczos, C.Pauli, W.BibcodeFock, V.Bargmann, V.Hamilton, W. R.American Journal of PhysicsLandau, L. D.Lifshitz E. M.Symon, K. R.Hermann, J.Bernoulli, J.Laplace, P. S.Gibbs, J. W.Runge, C.Lenz, W.Einstein, A.Le Verrier, U. J. J.Pais, A.Dirac, P. A. M.Schrödinger, E.Merzbacher, EugenMcIntosh H. V.Lie, S.Baez, John