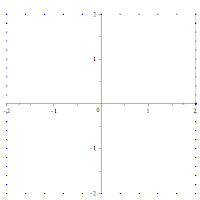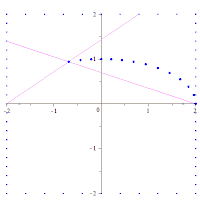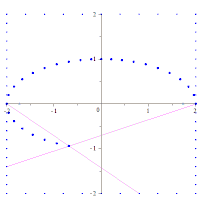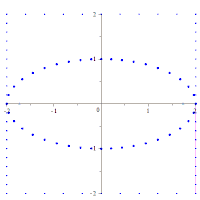
Ellipse
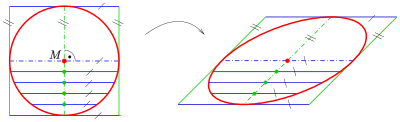
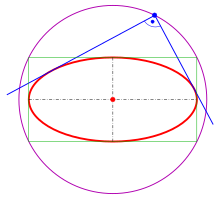
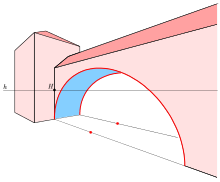
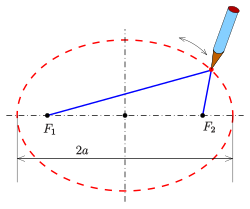
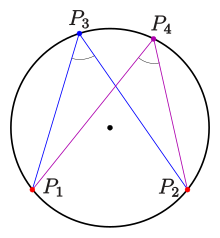
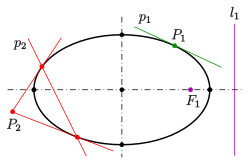
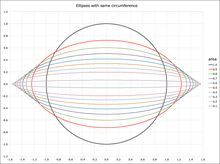
Ellipses have many similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded.The ellipse is also the simplest Lissajous figure formed when the horizontal and vertical motions are sinusoids with the same frequency: a similar effect leads to elliptical polarization of light in optics.An ellipse can be defined geometrically as a set or locus of points in the Euclidean plane: The midpointwith the x-axis, but has a geometric meaning due to Philippe de La Hire (see § Drawing ellipses below).The principle was known to the 5th century mathematician Proclus, and the tool now known as an elliptical trammel was invented by Leonardo da Vinci.The Byzantine architect Anthemius of Tralles (c. 600) described how this method could be used to construct an elliptical reflector,[13] and it was elaborated in a now-lost 9th-century treatise by Al-Ḥasan ibn Mūsā.[14] A similar method for drawing confocal ellipses with a closed string is due to the Irish bishop Charles Graves.A technical realization of the motion of the paper strip can be achieved by a Tusi couple (see animation).Most ellipsograph drafting instruments are based on the second paperstrip method.From Metric properties below, one obtains: The diagram shows an easy way to find the centers of curvatureof the rectangle is divided into n equal spaced line segments and this division is projected parallel with the diagonalone obtains the three-point form Analogously to the circle case, the equation can be written more clearly using vectors:[25]: 3 More generally, the arc length of a portion of the circumference, as a function of the angle subtended (or x coordinates of any two points on the upper half of the ellipse), is given by an incomplete elliptic integral.is the circumference of a circumscribed concentric circle passing through the endpoints of the ellipse's major axis, and the lower boundHowever, the general theory of straightedge-and-compass elliptic division appears to be unknown, unlike in the case of the circle and the lemniscate.Ellipses appear in triangle geometry as Ellipses appear as plane sections of the following quadrics: If the water's surface is disturbed at one focus of an elliptical water tank, the circular waves of that disturbance, after reflecting off the walls, converge simultaneously to a single point: the second focus.If the ellipse is rotated along its major axis to produce an ellipsoidal mirror (specifically, a prolate spheroid), this property holds for all rays out of the source.The same effect can be demonstrated with two reflectors shaped like the end caps of such a spheroid, placed facing each other at the proper distance.Examples are the National Statuary Hall at the United States Capitol (where John Quincy Adams is said to have used this property for eavesdropping on political matters); the Mormon Tabernacle at Temple Square in Salt Lake City, Utah; at an exhibit on sound at the Museum of Science and Industry in Chicago; in front of the University of Illinois at Urbana–Champaign Foellinger Auditorium; and also at a side chamber of the Palace of Charles V, in the Alhambra.Keplerian elliptical orbits are the result of any radially directed attraction force whose strength is inversely proportional to the square of the distance.(However, this conclusion ignores losses due to electromagnetic radiation and quantum effects, which become significant when the particles are moving at high speed.)Such is the case, for instance, of a long pendulum that is free to move in two dimensions; of a mass attached to a fixed point by a perfectly elastic spring; or of any object that moves under influence of an attractive force that is directly proportional to its distance from a fixed attractor.In electronics, the relative phase of two sinusoidal signals can be compared by feeding them to the vertical and horizontal inputs of an oscilloscope.Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times.Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form.Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage.[30] An example gear application would be a device that winds thread onto a conical bobbin on a spinning machine.The concept extends to an arbitrary number of elements of the random vector, in which case in general the iso-density contours are ellipsoids.[34][35] Drawing an ellipse as a graphics primitive is common in standard display libraries, such as the MacIntosh QuickDraw API, and Direct2D on Windows.[37] In 1970 Danny Cohen presented at the "Computer Graphics 1970" conference in England a linear algorithm for drawing ellipses and circles.Thus, the change in slope between each successive point is small, reducing the apparent "jaggedness" of the approximation.


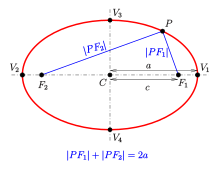
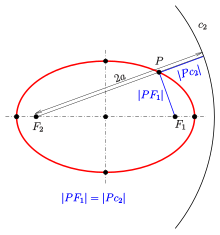
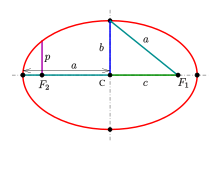
- a : semi-major axis,
- b : semi-minor axis,
- c : linear eccentricity,
- p : semi-latus rectum (usually ).


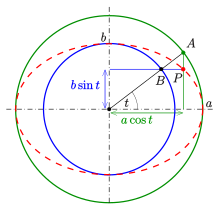


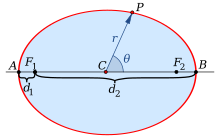
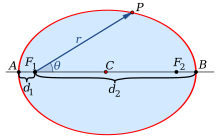
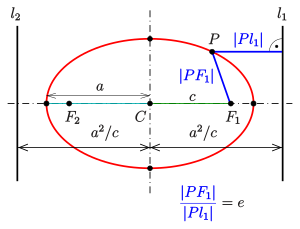

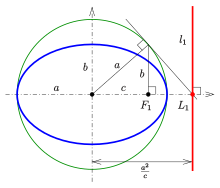
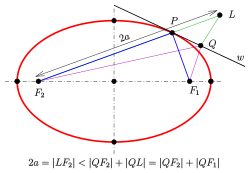
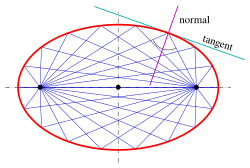






Ellipse (disambiguation)EllipsisEclipseEclipticmathematicsplane curvefocal pointscircleeccentricitylimiting caseparabolaalgebraicits perimetercircumferenceintegrationAnalyticallyclosedconic sectionhyperbolasunboundedcross sectionphysicsastronomyengineeringSolar Systembarycenterellipsoidsparallelperspective projectionLissajous figuresinusoidselliptical polarizationopticsApollonius of Pergalocus of pointsverticesDandelin spheresradicalssemi-major and semi-minor axesradius of curvatureparametric equationperpendicular vectorMatrix representation of conic sectionsanalytic geometryquadricCartesian planeimplicitdegenerate casesdeterminanttrigonometric functionseccentric anomalyPhilippe de La Hirereal projective linecomputer-aided designorthopticaffine transformationsmatrixconjugate diametersCramer's ruleequationrotatedpolar coordinatestrue anomalysemi-latus rectumline at infinityprojective planecircle inversionHesse normal formtriangle inequalityangle bisector theoremwhispering galleryOrthoptic (geometry)director circledescriptive geometryellipsographsProcluselliptical trammelLeonardo da VinciRytz's constructionde La Hiredrawing pinsAnthemius of TrallesAl-Ḥasan ibn MūsāCharles GravesTusi coupleBenjamin BramerdraftingFrench curveosculating circlesSteiner generation of a conic sectionpencilshypotrochoidinscribed angle theoremdot productsdeterminantsq-analogdot productbijectioninverse functionpole-polar relationInversive geometryintegralsflatteningPerimeter of an ellipsecomplete elliptic integral of the second kindelementary functionGauss's arithmetic-geometric meaninfinite seriesdouble factorialJames IvoryBesselKummerdouble-precision floating-pointSrinivasa Ramanujanapproximationsarc lengthelliptic integralcircumscribedconcentric circleinscribedrhombusstraightedge and compassthe case of the circlethe lemniscateLegendrecurvature


