Elliptic orbit
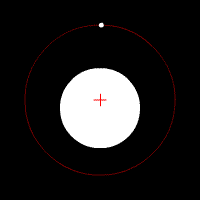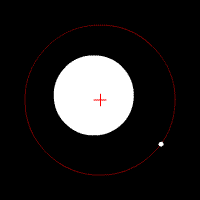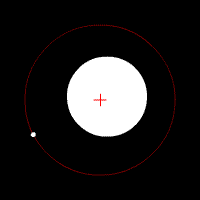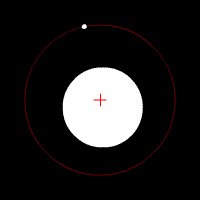
This includes the radial elliptic orbit, with eccentricity equal to 1.The relative position of one body with respect to the other also follows an elliptic orbit.Under standard assumptions, no other forces acting except two spherically symmetrical bodiesThe total energy of the orbit is given by where a is the semi major axis.Since gravity is a central force, the angular momentum is constant: At the closest and furthest approaches, the angular momentum is perpendicular to the distance from the mass orbited, therefore: The total energy of the orbit is given by[5] Substituting for v, the equation becomes This is true for r being the closest / furthest distance so two simultaneous equations are made, which when solved for E: SinceThe flight path angle is the angle between the orbiting body's velocity vector (equal to the vector tangent to the instantaneous orbit) and the local horizontal.Under standard assumptions of the conservation of angular momentum the flight path angleIf the eccentricity is less than 1 then the equation of motion describes an elliptical orbit.However, closed-form time-independent path equations of an elliptic orbit with respect to a central body can be determined from just an initial position (is the specific angular momentum of the orbiting body:[7] Then This can be done in cartesian coordinates using the following procedure: The general equation of an ellipse under the assumptions above is: Given: and Then:Now the result values fx, fy and a can be applied to the general ellipse equation above.This set of six variables, together with time, are called the orbital state vectors.The two most general cases with these 6 degrees of freedom are the elliptic and the hyperbolic orbit.Special cases with fewer degrees of freedom are the circular and parabolic orbit.Because at least six variables are absolutely required to completely represent an elliptic orbit with this set of parameters, then six variables are required to represent an orbit with any set of parameters.In the Solar System, planets, asteroids, most comets, and some pieces of space debris have approximately elliptical orbits around the Sun.For similar distances from the sun, wider bars denote greater eccentricity.A radial trajectory can be a double line segment, which is a degenerate ellipse with semi-minor axis = 0 and eccentricity = 1.In the case of point masses one full orbit is possible, starting and ending with a singularity.The velocities at the start and end are infinite in opposite directions and the potential energy is equal to minus infinity.The radial elliptic trajectory is the solution of a two-body problem with at some instant zero speed, as in the case of dropping an object (neglecting air resistance).The Babylonians were the first to realize that the Sun's motion along the ecliptic was not uniform, though they were unaware of why this was; it is today known that this is due to the Earth moving in an elliptic orbit around the Sun, with the Earth moving faster when it is nearer to the Sun at perihelion and moving slower when it is farther away at aphelion.[8] In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun at one focus, and described this in his first law of planetary motion.Later, Isaac Newton explained this as a corollary of his law of universal gravitation.
0.0 · 0.2 · 0.4 · 0.6 · 0.8



barycentergravitational potential wellOrbital mechanicsOrbital elementsArgument of periapsisEccentricityInclinationMean anomalyOrbital nodesSemi-major axisTrue anomalytwo-body orbitsCircular orbitTransfer orbitHohmann transfer orbitBi-elliptic transfer orbitParabolic orbitHyperbolic orbitRadial orbitDecaying orbitDynamical frictionEscape velocityKepler's equationKepler's laws of planetary motionOrbital periodOrbital velocitySurface gravitySpecific orbital energyVis-viva equationCelestial mechanicsHill spherePerturbationsSphere of influenceN-body orbitsLagrangian pointsHalo orbitsLissajous orbitsLyapunov orbitsEngineering and efficiencyMass ratioPayload fractionPropellant mass fractionTsiolkovsky rocket equationGravity assistOberth effectOrbital maneuverOrbit insertionastrodynamicsKepler orbitenergygravitational two-body problemnegative energysimilarHohmann transfer orbitsMolniya orbitstundra orbitsorbital speedstandard gravitational parameterhyperbolic trajectorycentral bodyvirial theoremspecific relative angular momentumOrbit equationorbiting bodyclosed-form solutionEccentric anomalyEccentricity vectorCartesian coordinatesorbital state vectorsSolar Systemplanetsasteroidscometsspace debrisperihelion and apheliondwarf planetsHalley's Cometperihelionaphelionorbital eccentricityradial trajectorydroppingBabylonianseclipticJohannes Keplerfirst law of planetary motionIsaac Newtonlaw of universal gravitationCharacteristic energyEllipseList of orbitsParabolic trajectoryCambridge University PressBibcodeButterworth-HeinemannorbitsCaptureCircularHighly ellipticalEscapeHorseshoeInclinedNon-inclinedKeplerLagrange pointOsculatingParkingPrograde / RetrogradeSynchronousGeocentricGeosynchronousGeostationaryGeostationary transferGraveyardHigh EarthLow EarthMedium EarthMolniyaNear-equatorialOrbit of the MoonSun-synchronousTransatmosphericTundraVery low EarthAreocentricAreosynchronous