Parabolic coordinates
A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.Parabolic coordinates have found many applications, e.g., the treatment of the Stark effect and the potential theory of the edges.are defined by the equations, in terms of Cartesian coordinates: The curves of constantform confocal parabolae that open upwards (i.e., towardsby substituting the scale factors into the general formulae found in orthogonal coordinates.The parabolic cylindrical coordinates are produced by projecting in theRotation about the symmetry axis of the parabolae produces a set of confocal paraboloids, the coordinate system of tridimensional parabolic coordinates.Expressed in terms of cartesian coordinates: where the parabolae are now aligned with theform confocal paraboloids that open upwards (i.e., towardsThe Riemannian metric tensor associated with this coordinate system is The three dimensional scale factors are: It is seen that the scale factorsThe infinitesimal volume element is then and the Laplacian is given by Other differential operators such asby substituting the scale factors into the general formulae found in orthogonal coordinates.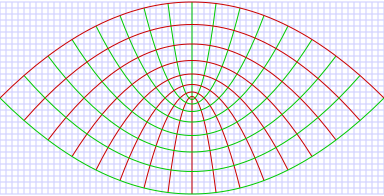

orthogonalcoordinate systemconfocalparabolasA three-dimensional versionsystemStark effectpotential theoryLaplacianorthogonal coordinatesCartesian coordinatesparabolic cylindrical coordinatesRiemannianmetric tensorOrthogonal coordinate systemCurvilinear coordinatesMorse PMFeshbach HMargenau HKorn TMEncyclopedia of MathematicsEMS PressOrthogonal coordinate systemsCartesianLog-polarBipolarEllipticCylindricalSphericalParabolicParaboloidalOblate spheroidalProlate spheroidalEllipsoidalElliptic cylindricalToroidalBisphericalBipolar cylindricalConical6-sphere

