Bell's theorem
Bell's theorem is a term encompassing a number of closely related results in physics, all of which determine that quantum mechanics is incompatible with local hidden-variable theories, given some basic assumptions about the nature of measurement.Often, these experiments have had the goal of "closing loopholes", that is, ameliorating problems of experimental design or set-up that could in principle affect the validity of the findings of earlier Bell tests.[3][4] The exact nature of the assumptions required to prove a Bell-type constraint on correlations has been debated by physicists and by philosophers.[5] Significantly, Bell-type theorems do not refer to any particular theory of local hidden variables, but instead show that quantum physics violates general assumptions behind classical pictures of nature.The original theorem proved by Bell in 1964 is not the most amenable to experiment, and it is convenient to introduce the genre of Bell-type inequalities with a later example.Consequently, if the experiment is repeated over many trials, with Victor preparing new pairs of particles, the absolute value of the average of the combinationBell's 1964 paper points out that under restricted conditions, local hidden-variable models can reproduce the predictions of quantum mechanics.Bell proves by example that these special cases can be explained in terms of hidden variables, then proceeds to show that the full range of possibilities involving intermediate angles cannot.Bell posited that a local hidden-variable model for these correlations would explain them in terms of an integral over the possible values of some hidden parameter"[14] Daniel Greenberger, Michael A. Horne, and Anton Zeilinger presented a four-particle thought experiment in 1990, which David Mermin then simplified to use only three particles.[22]: 196–201 The Kochen–Specker type of argument, using configurations of interlocking bases, can be combined with the idea of measuring entangled pairs that underlies Bell-type inequalities.The "EPR criterion of reality" posits that because the second half of the pair was not disturbed, that certainty must be due to a physical property belonging to it.This type of argument gained attention when an instance of it was advanced by John Conway and Simon Kochen under the name of the free will theorem.[31] As Bell pointed out, some predictions of quantum mechanics can be replicated in local hidden-variable models, including special cases of correlations produced from entanglement.In his 1932 textbook on quantum mechanics, the Hungarian-born polymath John von Neumann presented what he claimed to be a proof that there could be no "hidden parameters".The validity and definitiveness of von Neumann's proof were questioned by Hans Reichenbach, in more detail by Grete Hermann, and possibly in conversation though not in print by Albert Einstein.[note 3] (Simon Kochen and Ernst Specker rejected von Neumann's key assumption as early as 1961, but did not publish a criticism of it until 1967.His preferred argument relied on a principle of locality: The EPR thought experiment is similar, also considering two separated systems A and B described by a joint wave function.[43] The year before, Chien-Shiung Wu and Irving Shaknov had successfully measured polarizations of photons produced in entangled pairs, thereby making the Bohm version of the EPR thought experiment practically feasible.[49][50] The Kochen–Specker theorem refines this statement by constructing a specific finite subset of rays on which no such probability measure can be defined.He considered events where two kaons were produced traveling in opposite directions, and came to the conclusion that hidden variables could not explain the correlations that could be obtained in such situations.Because the journal did not provide free reprints of articles for the authors to distribute, however, Bell had to spend the money he received to buy copies that he could send to other physicists.[49][53] In that paper, Bell argued that because an explanation of quantum phenomena in terms of hidden variables would require nonlocality, the EPR paradox "is resolved in the way which Einstein would have liked least.The purpose of the experiment is to test whether nature can be described by local hidden-variable theory, which would contradict the predictions of quantum mechanics.The locality loophole is opened when the detections are not done with a spacelike separation, making it possible for the result of one measurement to influence the other without contradicting relativity."[67] These efforts to experimentally validate violations of the Bell inequalities would later result in Clauser, Aspect, and Anton Zeilinger being awarded the 2022 Nobel Prize in Physics.Maximilian Schlosshauer, Johannes Kofler, and Zeilinger write that Bell inequalities provide "a wonderful example of how we can have a rigorous theoretical result tested by numerous experiments, and yet disagree about the implications.[70][71] For example, Roland Omnès argues for the rejection of hidden variables and concludes that "quantum mechanics is probably as realistic as any theory of its scope and maturity ever will be".[72]: 531 Likewise, Rudolf Peierls took the message of Bell's theorem to be that, because the premise of locality is physically reasonable, "hidden variables cannot be introduced without abandoning some of the results of quantum mechanics".[note 5] They are ready to give up locality, explaining the violation of Bell's inequality by means of a non-local hidden variable theory, in which the particles exchange information about their states.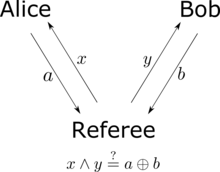

The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation (a or b) can be set by the experimenter. Emerging signals from each channel are detected and coincidences of four types (++, −−, +− and −+) counted by the coincidence monitor.
Bell testphysicsquantum mechanicslocal hidden-variable theoriesprinciple of localityparticlephysical fieldsspeed of lightHidden variablesJohn Stewart BellEinstein–Podolsky–Rosen paradoxquantum entanglementinequalityJohn ClauserStuart FreedmanBell testsphilosophersinterpretations of quantum mechanicsAlice and BobCHSH inequalityqubitsBell statePauli matricesmeasurementsBorn ruleTsirelson bounda game in which Alice and Bob try to coordinate their actionslogical ANDlogical XORDavid Bohmspin singlet stateStern–Gerlach devicevectorcorrelationprobability density functionGHZ experimentDaniel GreenbergerMichael A. HorneAnton ZeilingerDavid Merminquantum pseudo-telepathyKochen–Specker theoremHilbert spaceFree will theoremJohn ConwaySimon KochenqutritsAsher PeresSpekkens toy modelWerner stateReinhard WernerWerner statesunitariestensor-productRobert Spekkenstoy modelmonogamyEPR paradoxHistory of quantum mechanics1932 textbook on quantum mechanicsJohn von NeumannHans ReichenbachGrete HermannErnst SpeckerSchrödinger equationChien-Shiung WuGeorge MackeyAndrew M. GleasonGleason's theoremspecial relativityTsung-Dao Leepage chargesPhysics Physique ФизикаAlain Aspectfirst Bell testlocal hidden-variable theoryNobel Prize in PhysicsCopenhagen-type interpretationscounterfactual definitenessRoland OmnèsRudolf Peierlsconsistent historiesMany-worlds interpretationEverettaction at a distancehidden variable theoryBohm interpretationtransactional interpretationSuperdeterminismfree willGerard 't HooftEinstein's thought experimentsEpistemological LettersFundamental Fysiks GroupLeggett inequalityLeggett–Garg inequalityMermin's deviceMott problemPBR theoremQuantum contextualityQuantum nonlocalityRenninger negative-result experimentPaul DiracDavid HilbertHermann Weylseparableself-adjointoperatorsdeterministicspin-1unit sphereconnectedE. T. JaynesBell, John S.Nobel PrizeThe Royal Swedish Academy of SciencesNatureBibcodeWolchover, NatalieQuanta MagazineShimony, AbnerZalta, Edward N.Stanford Encyclopedia of PhilosophyNielsen, Michael A.Chuang, Isaac L.Quantum Computation and Quantum Information