Connected space
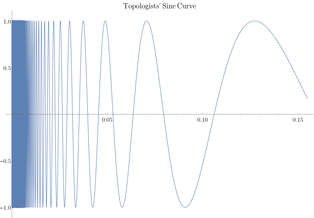
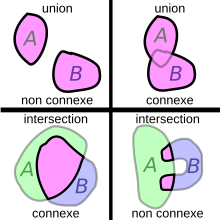
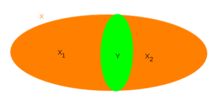
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets.Another related notion is locally connected, which neither implies nor follows from connectedness.is said to be disconnected if it is the union of two disjoint non-empty open sets.Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice.the following conditions are equivalent: Historically this modern formulation of the notion of connectedness (in terms of no partition ofinto two separated sets) first appeared (independently) with N.J. Lennes, Frigyes Riesz, and Felix Hausdorff at the beginning of the 20th century.the union of any collection of connected subsets such that each containsThe maximal connected subsets (ordered by inclusionIt follows that, in the case where their number is finite, each component is also an open subset.However, if their number is infinite, this might not be the case; for instance, the connected components of the set of the rational numbers are the one-point sets (singletons), which are not open.[1][better source needed] A space in which all components are one-point sets is called totally disconnected.The resulting space, with the quotient topology, is totally disconnected.An example of a space that is not connected is a plane with an infinite line deleted from it.Other examples of disconnected spaces (that is, spaces which are not connected) include the plane with an annulus removed, as well as the union of two disjoint closed disks, where all examples of this paragraph bear the subspace topology induced by two-dimensional Euclidean space.A path-connected space is a stronger notion of connectedness, requiring the structure of a path.For non-empty spaces, this is equivalent to the statement that there is a path joining any two points inThe converse is not always true: examples of connected spaces that are not path-connected include the extended long lineare connected if and only if they are path-connected; these subsets are the intervals and rays ofAdditionally, connectedness and path-connectedness are the same for finite topological spaces.is said to be arc-connected or arcwise connected if any two topologically distinguishable points can be joined by an arc, which is an embeddingEvery Hausdorff space that is path-connected is also arc-connected; more generally this is true for aAn example of a space which is path-connected but not arc-connected is given by the line with two origins; its two copies ofis locally connected if and only if every component of every open set ofMore generally, any topological manifold is locally path-connected.A simple example of a locally connected (and locally path-connected) space that is not connected (or path-connected) is the union of two separated intervals inis disconnected (and thus can be written as a union of two open setsSo it can be written as the union of two disjoint open sets, e.g.As a consequence, a notion of connectedness can be formulated independently of the topology on a space.However, every graph can be canonically made into a topological space, by treating vertices as points and edges as copies of the unit interval (see topological graph theory#Graphs as topological spaces).The deleted comb space furnishes such an example, as does the above-mentioned topologist's sine curve.
subsetssimply connectedtopologymathematicstopological spacedisjointnon-emptyopen subsetstopological propertiessubspace
n
{\displaystyle n}
-connectedlocally connectedsubsetempty setclopen setsboundaryseparated setsdiscrete topologyFrigyes RieszFelix Hausdorffmaximalinclusionpartitionclosed subsetrational numberssingletonsclopenquasi-componenttotally disconnectedopen setsquotient topologyHausdorffstandardsubspace topologyconvex subsetEuclidean planereal numbersSorgenfrey linetopological vector spaceHilbert spaceBanach spacediscrete topological spacediscrete two-point spacediscrete valuation ringSierpiński spaceCantor sethomotopy equivalenttopologist's sine curvegeneral linear grouplocal ringfinitely generated projective moduleidempotentannulusunit intervalequivalence classequivalence relationlong linereal lineif and only ifintervalsfinite topological spacestopologically distinguishableembeddingHausdorff space
Δ
{\displaystyle \Delta }
-Hausdorff spaceline with two originsLocally connected spacetopological manifoldseparatedEuclidean topologyinduceddisjoint unionsquotient spaceset differenceintermediate value theoremclosureclosedquotientproductmanifoldGraphs5-cycletopological spaceshyperconnected spacessimply connected spacecontractible spacedeleted comb spaceConnected component (graph theory)Connectedness locusDomain (mathematical analysis)Extremally disconnected spacen-connectedUniformly connected spacePixel connectivityGeorge F. SimmonsCharles WeibelStack ExchangeMunkres, James R.Weisstein, Eric W.MathWorldEncyclopedia of MathematicsEMS PressGeneral (point-set)AlgebraicCombinatorialContinuumDifferentialGeometriclow-dimensionalHomologycohomologySet-theoreticDigitalOpen setClosed setInteriorContinuitycompactmetricuniformHomotopyhomotopy groupfundamental groupSimplicial complexCW complexPolyhedral complex