Lagrange multiplier
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equation constraints (i.e., subject to the condition that one or more equations have to be satisfied exactly by the chosen values of the variables).[6] The great advantage of this method is that it allows the optimization to be solved without explicit parameterization in terms of the constraints.As a result, the method of Lagrange multipliers is widely used to solve challenging constrained optimization problems.Further, the method of Lagrange multipliers is generalized by the Karush–Kuhn–Tucker conditions, which can also take into account inequality constraints of the formThe Lagrange multiplier theorem states that at any local maximum (or minimum) of the function evaluated under the equality constraints, if constraint qualification applies (explained below), then the gradient of the function (at that point) can be expressed as a linear combination of the gradients of the constraints (at that point), with the Lagrange multipliers acting as coefficients.For the case of only one constraint and only two choice variables (as exemplified in Figure 1), consider the optimization problemThe global optimum can be found by comparing the values of the original objective function at the points satisfying the necessary and locally sufficient conditions.The method of Lagrange multipliers relies on the intuition that at a maximum, f(x, y) cannot be increasing in the direction of any such neighboring point that also has g = 0.If it were, we could walk along g = 0 to get higher, meaning that the starting point wasn't actually the maximum.The fact that solutions of the method of Lagrange multipliers are not necessarily extrema of the Lagrangian, also poses difficulties for numerical optimization.The method of Lagrange multipliers can be extended to solve problems with multiple constraints using a similar argument.Consider a paraboloid subject to two line constraints that intersect at a single point.For example, by parametrising the constraint's contour line, that is, if the Lagrangian expression isSo, λk is the rate of change of the quantity being optimized as a function of the constraint parameter.As examples, in Lagrangian mechanics the equations of motion are derived by finding stationary points of the action, the time integral of the difference between kinetic and potential energy.Thus, the force on a particle due to a scalar potential, F = −∇V, can be interpreted as a Lagrange multiplier determining the change in action (transfer of potential to kinetic energy) following a variation in the particle's constrained trajectory.For example, in economics the optimal profit to a player is calculated subject to a constrained space of actions, where a Lagrange multiplier is the change in the optimal value of the objective function (profit) due to the relaxation of a given constraint (e.g. through a change in income); in such a context[15] Sufficient conditions for a constrained local maximum or minimum can be stated in terms of a sequence of principal minors (determinants of upper-left-justified sub-matrices) of the bordered Hessian matrix of second derivatives of the Lagrangian expression.are still lines of slope −1, and the points on the circle tangent to these level sets are again[4][17] Unfortunately, many numerical optimization techniques, such as hill climbing, gradient descent, some of the quasi-Newton methods, among others, are designed to find local maxima (or minima) and not saddle points.For this reason, one must either modify the formulation to ensure that it's a minimization problem (for example, by extremizing the square of the gradient of the Lagrangian as below), or else use an optimization technique that finds stationary points (such as Newton's method without an extremum seeking line search) and not necessarily extrema.(This problem is somewhat untypical because there are only two values that satisfy this constraint, but it is useful for illustration purposes because the corresponding unconstrained function can be visualized in three dimensions.)First, we compute the partial derivative of the unconstrained problem with respect to each variable:Thus, the "square root" may be omitted from these equations with no expected difference in the results of optimization.)however, the critical points in h occur at local minima, so numerical optimization techniques can be used to find them.The usual way to determine an optimal solution is achieved by maximizing some function, where the constraints are enforced using Lagrangian multipliers.[19][20][21][22] Methods based on Lagrange multipliers have applications in power systems, e.g. in distributed-energy-resources (DER) placement and load shedding.[23] The method of Lagrange multipliers applies to constrained Markov decision processes.[24] It naturally produces gradient-based primal-dual algorithms in safe reinforcement learning.[25] Considering the PDE problems with constraints, i.e., the study of the properties of the normalized solutions, Lagrange multipliers play an important role.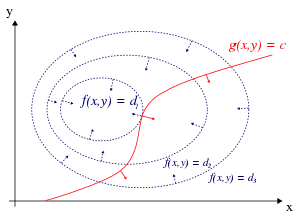







Lagrangian (physics)mathematical optimizationmaxima and minimafunctionequation constraintsequationsvariablesJoseph-Louis Lagrangederivative testinner productdot productstationary pointspartial derivativessaddle pointdefinitenessbordered Hessian matrixparameterizationKarush–Kuhn–Tucker conditionsobjective functiongradientlinear combinationcoefficientsdirectional derivativeoptimization problemstationary pointnecessary conditionalso existcandidate solutioncontourscritical pointsHamiltonianoptimal controlPontryagin's minimum principleparaboloidlevel setdifferentiable manifoldexterior derivativesmooth manifoldregular valueexterior derivativesexterior productdecomposable elementsLagrangian mechanicsactioncostate equationsenvelope theoremmarginal costshadow priceBordered HessianHessian matrixfeasible setlevel setsglobal maximumglobal minimumlocal minimumlocal maximumindefinite matrixinformation entropyleast structuredShannon entropysaddle pointshill climbinggradient descentquasi-Newton methodsNewton's methodline searchcostatenonlinear programmingmathematical economicsgeneral equilibrium modelsutility maximizationprofit maximizationbudget constraintsproduction constraintspower systemsNormalized solutionsAdjustment of observationsDualityGittins indexLagrange multipliers on Banach spacesLagrange multiplier testLagrangian relaxationProtter, Murray H.Morrey, Charles B. Jr.Mathematics MagazineLuenberger, David G.Bertsekas, Dimitri P.Encyclopedia of MathematicsEMS PressLemaréchal, ClaudeDixit, Avinash K.Chiang, Alpha C.Heath, Michael T.American Mathematical MonthlyKamien, M. I.Schwartz, N. L.BibcodeInstitute of Electronic and Electrical EngineersRoutledgeHestenes, Magnus R.calculus of variationsKansas State UniversityUniversity of MarylandUniversity of California, BerkeleyWolfram ResearchMassachusetts Institute of TechnologyCalculusPrecalculusBinomial theoremConcave functionContinuous functionFactorialFinite differenceFree variables and bound variablesGraph of a functionLinear functionRadianRolle's theoremSecantTangentLimitsIndeterminate formLimit of a functionOne-sided limitLimit of a sequenceOrder of approximation