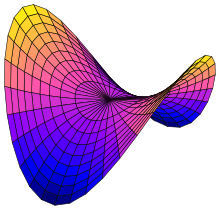
Saddle point

[2] An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and a relative maximum along the crossing axis.The name derives from the fact that the prototypical example in two dimensions is a surface that curves up in one direction, and curves down in a different direction, resembling a riding saddle.In terms of contour lines, a saddle point in two dimensions gives rise to a contour map with a pair of lines intersecting at the point.Such intersections are rare in actual ordnance survey maps, as the height of the saddle point is unlikely to coincide with the integer multiples used in such maps.Instead, the saddle point appears as a blank space in the middle of four sets of contour lines that approach and veer away from it.The critical contour lines generally do not have to intersect orthogonally.In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/surface/etc.The Pringles potato chip or crisp is an everyday example of a hyperbolic paraboloid shape.Saddle surfaces have negative Gaussian curvature which distinguish them from convex/elliptical surfaces which have positive Gaussian curvature.For a second-order linear autonomous system, a critical point is a saddle point if the characteristic equation has one positive and one negative real eigenvalue.[4] In optimization subject to equality constraints, the first-order conditions describe a saddle point of the Lagrangian.
A saddle point (in red) on the graph of z = x 2 − y 2 ( hyperbolic paraboloid )
A riding saddle
Saddle point between two hills (the intersection of the figure-eight z -contour)
Saddle point on the contour plot is the point where level curves cross
The plot of y = x 3 with a saddle point at 0
Hyperbolic paraboloid
A model of an elliptic hyperboloid of one sheet
A monkey saddle
Saddle PointSaddle (landform)mathematicssurfacegraph of a functionslopesorthogonalcritical pointlocal extremumminimummaximumsaddlecontour linesstationary pointHessian matrixnull matrixsmooth functionhypersurfaceneighborhoodtangent spacepoint of inflectionHyperbolic paraboloidelliptic hyperboloidmonkey saddlesmooth surfaceEuclidean spacehyperboloid of one sheetPringlesGaussian curvaturezero sumequilibriumcharacteristic equationeigenvalueLagrangiandynamical systemsdifferentiable mapunit circleperiodic pointstableunstable manifoldsdimensionSaddle-point methodLaplace's methodMaximum and minimumDerivative testHyperbolic equilibrium pointHyperbolic geometryMinimax theoremMax–min inequalityMountain pass theoremChiang, Alpha C.McGraw-HillBuck, R. CreightonHilbert, DavidCohn-Vossen, StephanChelseaWidder, D. V.