Feasible region
In mathematical optimization and computer science, a feasible region, feasible set, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints.The feasible set of the problem is separate from the objective function, which states the criterion to be optimized and which in the above example isIn many problems, the feasible set reflects a constraint that one or more variables must be non-negative.In linear programming problems, the feasible set is a convex polytope: a region in multidimensional space whose boundaries are formed by hyperplanes and whose corners are vertices.Convex feasible sets arise in many types of problems, including linear programming problems, and they are of particular interest because, if the problem has a convex objective function that is to be minimized, it will generally be easier to solve in the presence of a convex feasible set and any local optimum will also be a global optimum.In linear programming problems with n variables, a necessary but insufficient condition for the feasible set to be bounded is that the number of constraints be at least n + 1 (as illustrated by the above example).If the feasible set is unbounded, there may or may not be an optimum, depending on the specifics of the objective function.Constraint satisfaction is the process of finding a point in the feasible set.[3] In calculus, an optimal solution is sought using the first derivative test: the first derivative of the function being optimized is equated to zero, and any values of the choice variable(s) that satisfy this equation are viewed as candidate solutions (while those that do not are ruled out as candidates).First, it might give a minimum when a maximum is being sought (or vice versa), and second, it might give neither a minimum nor a maximum but rather a saddle point or an inflection point, at which a temporary pause in the local rise or fall of the function occurs.In the simplex method for solving linear programming problems, a vertex of the feasible polytope is selected as the initial candidate solution and is tested for optimality; if it is rejected as the optimum, an adjacent vertex is considered as the next candidate solution.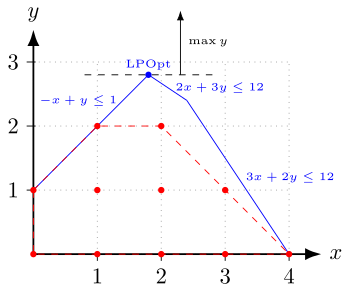



integer constraintslinear programmingpolyhedronmathematical optimizationcomputer scienceoptimization problemconstraintsinequalitiesequalitiesintegercandidate solutionsobjective functioninteger programmingconvexpolytopemultidimensional spacehyperplanesverticesConstraint satisfactionConvex optimizationconvex objective functionlocal optimumglobal optimumempty setbounded or unboundednecessary but insufficient conditionoptimizationmathematicssearch algorithmsmembergenetic algorithmfirst derivative testfirst derivativesaddle pointinflection pointsecond derivative testantiderivativesmonomialsCavalieri's quadrature formulasimple polygonsimplex methodvertex