Galilean transformation
In physics, a Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics.These transformations together with spatial rotations and translations in space and time form the inhomogeneous Galilean group (assumed throughout below).This is the passive transformation point of view.The equations below are only physically valid in a Newtonian framework, and not applicable to coordinate systems moving relative to each other at speeds approaching the speed of light.Galileo formulated these concepts in his description of uniform motion.[1] The topic was motivated by his description of the motion of a ball rolling down a ramp, by which he measured the numerical value for the acceleration of gravity near the surface of the Earth.Although the transformations are named for Galileo, it is the absolute time and space as conceived by Isaac Newton that provides their domain of definition.In essence, the Galilean transformations embody the intuitive notion of addition and subtraction of velocities as vectors.The notation below describes the relationship under the Galilean transformation between the coordinates (x, y, z, t) and (x′, y′, z′, t′) of a single arbitrary event, as measured in two coordinate systems S and S′, in uniform relative motion (velocity v) in their common x and x′ directions, with their spatial origins coinciding at time t = t′ = 0:[2][3][4][5] Note that the last equation holds for all Galilean transformations up to addition of a constant, and expresses the assumption of a universal time independent of the relative motion of different observers.In the language of linear algebra, this transformation is considered a shear mapping, and is described with a matrix acting on a vector.With motion parallel to the x-axis, the transformation acts on only two components: Though matrix representations are not strictly necessary for Galilean transformation, they provide the means for direct comparison to transformation methods in special relativity.The Galilean symmetries can be uniquely written as the composition of a rotation, a translation and a uniform motion of spacetime.A general point in spacetime is given by an ordered pair (x, t).A translation is given by where a ∈ R3 and s ∈ R. A rotation is given by where R : R3 → R3 is an orthogonal transformation.[6] Two Galilean transformations G(R, v, a, s) and G(R' , v′, a′, s′) compose to form a third Galilean transformation, The set of all Galilean transformations Gal(3) forms a group with composition as the group operation.The group is sometimes represented as a matrix group with spacetime events (x, t, 1) as vectors where t is real and x ∈ R3 is a position in space.The action is given by[7] where s is real and v, x, a ∈ R3 and R is a rotation matrix.The composition of transformations is then accomplished through matrix multiplication.Care must be taken in the discussion whether one restricts oneself to the connected component group of the orthogonal transformations.The identity component is denoted SGal(3).Since the transformations depend continuously on s, v, R, a, Gal(3) is a continuous group, also called a topological group.The structure of Gal(3) can be understood by reconstruction from subgroups.The Lie algebra of the Galilean group is spanned by H, Pi, Ci and Lij (an antisymmetric tensor), subject to commutation relations, where H is the generator of time translations (Hamiltonian), Pi is the generator of translations (momentum operator), Ci is the generator of rotationless Galilean transformations (Galileian boosts),[8] and Lij stands for a generator of rotations (angular momentum operator).[9] Formally, renaming the generators of momentum and boost of the latter as in where c is the speed of light (or any unbounded function thereof), the commutation relations (structure constants) in the limit c → ∞ take on the relations of the former.Generators of time translations and rotations are identified.In matrix form, for d = 3, one may consider the regular representation (embedded in GL(5; R), from which it could be derived by a single group contraction, bypassing the Poincaré group),The infinitesimal group element is then One may consider[10] a central extension of the Lie algebra of the Galilean group, spanned by H′, P′i, C′i, L′ij and an operator M: The so-called Bargmann algebra is obtained by imposing, such that M lies in the center, i.e. commutes with all other operators.In full, this algebra is given as and finally where the new parameterThis extension and projective representations that this enables is determined by its group cohomology.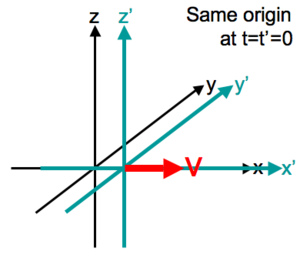
physicsreference framesNewtonian physicsgroup of motionsGalilean relativitypassive transformationspecial relativityLorentz transformationsPoincaré transformationsgroup contractionclassical limitspeed of lightGalileoaccelerationgravityabsolute time and spaceIsaac Newtonvectorsvelocitylinear algebrashear mappingcompositionorthogonal transformationLie groupdimensioncomposespacetimeactionrotation matrixmatrix multiplicationcontinuous groupsemidirect productnormal subgroupLie algebraGalilean groupspannedantisymmetric tensorcommutation relationsHamiltonianmomentum operatorangular momentum operatorcentercommutesprojective representationsGalilean invarianceRepresentation theory of the Galilean groupGalilei-covariant tensor formulationPoincaré groupLorentz groupLagrangian and Eulerian coordinatesArnold, V. I.Bargmann, V.Copernicus, NicolausKepler, JohannesGalilei, GalileoNewton, IsaacEinstein, AlbertHawking, StephenRunning PressElsevierDiscourses and Mathematical Demonstrations Relating to Two New SciencesHenry CrewDover PublicationsBibcodeGalileo GalileiObservational astronomyGalileo affairGalileo's escapementGalilean moonsLeaning Tower of Pisa experimentPhases of VenusCelatoneThermoscopeDe motu antiquioraSidereus NunciusLetters on SunspotsLetter to Benedetto CastelliLetter to the Grand Duchess ChristinaDiscourse on the TidesDiscourse on CometsThe AssayerDialogue Concerning the Two Chief World SystemsTwo New SciencesVincenzo GalileiMichelagnolo GalileiVincenzo GambaMaria CelesteMarina GambaAnd yet it movesVilla Il GioielloGalileo's paradoxGalileo's shipSectorMuseo GalileoGalileo's telescopesGalileo's objective lensTribune of GalileoGalileo thermometerGalileo projectspacecraftGalileo Galilei AirportGalileo National TelescopeAstronomers MonumentLife of Galileo (1943 play)Lamp At Midnight (1947 play)Galileo (1968 film)Galileo (1975 film)Starry Messenger (1996 book)Galileo's Daughter: A Historical Memoir of Science, Faith, and Love (1999 book)Galileo Galilei (2002 opera)Galileo's Dream (2009 novel)RelativitySpecialrelativityPrinciple of relativityDoubly special relativityFrame of referenceHyperbolic orthogonalityRapidityMaxwell's equationsProper lengthProper timeProper accelerationRelativistic massLorentz transformationTextbooksTime dilation