Quantum state
Two broad categories are Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states.Similarly, quantum states consist of sets of dynamical variables that evolve under equations of motion.However, the values derived from quantum states are complex numbers, quantized, limited by uncertainty relations,[1]: 159 and only provide a probability distribution for the outcomes for a system.Simultaneous measurement of a complete set of compatible variables prepares the system in a unique state.[1]: 196 Whatever the input quantum state might be, repeated identical measurements give consistent values.[1]: 204 The same physical quantum state can be expressed mathematically in different ways called representations.Representations are analogous to coordinate systems[1]: 244 or similar mathematical devices like parametric equations.This allows many elegant concepts of quantum mechanics to be expressed and to be applied even in cases where no classical analog exists.Preparing a system by measuring the complete set of compatible observables produces a pure quantum state.Wave function solutions of Schrödinger's equations of motion for operators corresponding to measurements can readily be expressed as pure states; they must be combined with statistical weights matching experimental preparation to compute the expected probability distribution.These solution states, called eigenstates, are labeled with quantized values, typically quantum numbers.The postulates of quantum mechanics state that pure states, at a given time t, correspond to vectors in a separable complex Hilbert space, while each measurable physical quantity (such as the energy or momentum of a particle) is associated with a mathematical operator called the observable.On the other hand, a pure state described as a superposition of multiple different eigenstates does in general have quantum uncertainty for the given observable.A pure quantum state can be represented by a ray in a projective Hilbert space over the complex numbers, while mixed states are represented by density matrices, which are positive semidefinite operators that act on Hilbert spaces.[8] Before a particular measurement is performed on a quantum system, the theory gives only a probability distribution for the outcome, and the form that this distribution takes is completely determined by the quantum state and the linear operators describing the measurement.Probability distributions for different measurements exhibit tradeoffs exemplified by the uncertainty principle: a state that implies a narrow spread of possible outcomes for one experiment necessarily implies a wide spread of possible outcomes for another.Statistical mixtures represent the degree of knowledge whilst the uncertainty within quantum mechanics is fundamental.Moreover, in contrast to classical mechanics, it is unavoidable that performing a measurement on the system generally changes its state.Another feature of quantum states becomes relevant if we consider a physical system that consists of multiple subsystems; for example, an experiment with two particles rather than one.These entangled states lead to experimentally testable properties (Bell's theorem) that allow us to distinguish between quantum theory and alternative classical (non-quantum) models.One can take the observables to be dependent on time, while the state σ was fixed once at the beginning of the experiment.One can, equivalently, treat the observables as fixed, while the state of the system depends on time; that is known as the Schrödinger picture.Most particles possess a kind of intrinsic angular momentum that does not appear at all in classical mechanics and arises from Dirac's relativistic generalization of the theory.For a given particle, the choice of representation (and hence the range of possible values of the spin observable) is specified by a non-negative number S that, in units of the reduced Planck constant ħ, is either an integer (0, 1, 2, ...) or a half-integer (1/2, 3/2, 5/2, ...).As a consequence, the quantum state of a particle with spin is described by a vector-valued wave function with values in C2S+1.Electrons are fermions with S = 1/2, photons (quanta of light) are bosons with S = 1 (although in the vacuum they are massless and can't be described with Schrödinger mechanics).In the first case, there could theoretically be another person who knows the full history of the system, and therefore describe the same system as a pure state; in this case, the density matrix is simply used to represent the limited knowledge of a quantum state.can be always represented as the partial trace of a pure quantum state (called a purification) on a larger bipartite systemThe rules for measurement in quantum mechanics are particularly simple to state in terms of density matrices.For a discussion of conceptual aspects and a comparison with classical states, see: For a more detailed coverage of mathematical aspects, see: For a discussion of purifications of mixed quantum states, see Chapter 2 of John Preskill's lecture notes for Physics 219 at Caltech.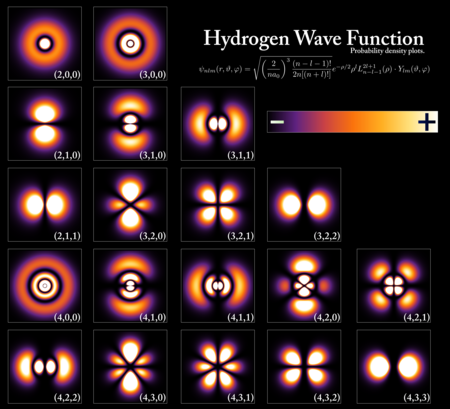
Quantum mechanicsSchrödinger equationIntroductionGlossaryHistoryClassical mechanicsOld quantum theoryBra–ket notationHamiltonianInterferenceComplementarityDecoherenceEntanglementEnergy levelMeasurementNonlocalityQuantum numberSuperpositionSymmetryTunnellingUncertaintyWave functionCollapseBell's inequalityCHSH inequalityDavisson–GermerDouble-slitElitzur–VaidmanFranck–HertzLeggett inequalityLeggett–Garg inequalityMach–ZehnderPopperQuantum eraserDelayed-choiceSchrödinger's catStern–GerlachWheeler's delayed-choiceOverviewHeisenbergInteractionMatrixPhase-spaceSchrödingerSum-over-histories (path integral)Klein–GordonRydbergInterpretationsBayesianConsistent historiesCopenhagende Broglie–BohmEnsembleHidden-variableSuperdeterminismMany-worldsObjective-collapseQuantum logicRelationalTransactionalVon Neumann–WignerRelativistic quantum mechanicsQuantum field theoryQuantum information scienceQuantum computingQuantum chaosEPR paradoxDensity matrixScattering theoryQuantum statistical mechanicsQuantum machine learningAharonovBlackettde BroglieComptonDavissonEhrenfestEinsteinEverettFeynmanGlauberGutzwillerHilbertJordanKramersLandauMoseleyMillikanPlanckSimmonsSommerfeldvon NeumannWignerZeemanZeilingerquantum physicswave functionscoherent statesstationary statesquantum vacuum statescomplex numbersuncertainty relationsprobability distributiondouble-slit experimentcomplete set of compatible variablesequations of motionMeasurement in quantum mechanicsuncertainty principleparametric equationsvector spacemomentumdegrees of freedomSchrödinger's equations of motionProbability densitieseigenstatesquantum numberselectronhydrogen atomprincipal quantum numberangular momentum quantum numbermagnetic quantum numberStern–Gerlach experimentcomplexpostulates of quantum mechanicsvectorsseparable