Coordinate descent
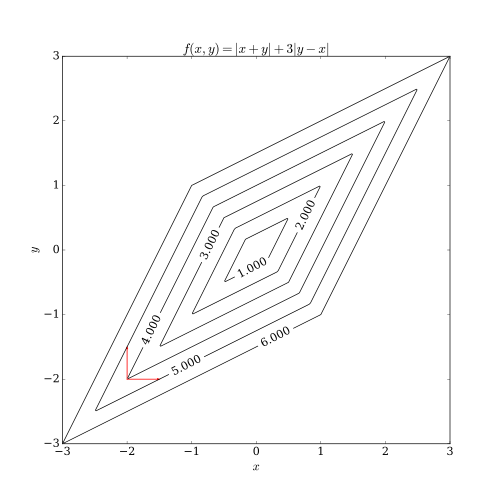
A line search along the coordinate direction can be performed at the current iterate to determine the appropriate step size.can be achieved by minimizing it along one direction at a time, i.e., solving univariate (or at least much simpler) optimization problems in a loop.By doing line search in each iteration, one automatically has It can be shown that this sequence has similar convergence properties as steepest descent.No improvement after one cycle of line search along coordinate directions implies a stationary point is reached.In the case of a continuously differentiable function F, a coordinate descent algorithm can be sketched as:[1] The step size can be chosen in various ways, e.g., by solving for the exact minimizer of f(xi) = F(x) (i.e., F with all variables but xi fixed), or by traditional line search criteria.The following picture shows that coordinate descent iteration may get stuck at a non-stationary point if the level curves of the function are not smooth.[4][5][6] Coordinate descent algorithms are popular with practitioners owing to their simplicity, but the same property has led optimization researchers to largely ignore them in favor of more interesting (complicated) methods.[1] An early application of coordinate descent optimization was in the area of computed tomography[7] where it has been found to have rapid convergence[8] and was subsequently used for clinical multi-slice helical scan CT reconstruction.[9] A cyclic coordinate descent algorithm (CCD) has been applied in protein structure prediction.[10] Moreover, there has been increased interest in the use of coordinate descent with the advent of large-scale problems in machine learning, where coordinate descent has been shown competitive to other methods when applied to such problems as training linear support vector machines[11] (see LIBLINEAR) and non-negative matrix factorization.

optimization algorithmfunctioncoordinateline searchlocal minimumcontinuously differentiablesketchedsmoothstationary pointmachine learningsupport vector machinesLIBLINEARnon-negative matrix factorizationAdaptive coordinate descentConjugate gradientGradient descentMathematical optimizationNewton's methodStochastic gradient descentBibcodeCiteSeerXNesterov, YuriiOptimizationAlgorithmsmethodsheuristicsUnconstrained nonlinearFunctionsGolden-section searchPowell's methodNelder–Mead methodSuccessive parabolic interpolationGradientsConvergenceTrust regionWolfe conditionsQuasi–NewtonBerndt–Hall–Hall–HausmanBroyden–Fletcher–Goldfarb–ShannoL-BFGSDavidon–Fletcher–PowellSymmetric rank-one (SR1)Other methodsGauss–NewtonGradientMirrorLevenberg–MarquardtPowell's dog leg methodTruncated NewtonHessiansConstrained nonlinearBarrier methodsPenalty methodsAugmented Lagrangian methodsSequential quadratic programmingSuccessive linear programmingConvex optimizationConvex minimizationCutting-plane methodReduced gradient (Frank–Wolfe)Subgradient methodLinearquadraticAffine scalingEllipsoid algorithm of KhachiyanProjective algorithm of KarmarkarBasis-exchangeSimplex algorithm of DantzigRevised simplex algorithmCriss-cross algorithmPrincipal pivoting algorithm of LemkeActive-set methodCombinatorialApproximation algorithmDynamic programmingGreedy algorithmInteger programmingBranch and boundGraph algorithmsMinimum spanning treeBorůvkaKruskalShortest pathBellman–FordDijkstraFloyd–WarshallNetwork flowsEdmonds–KarpFord–FulkersonPush–relabel maximum flowMetaheuristicsEvolutionary algorithmHill climbingLocal searchParallel metaheuristicsSimulated annealingSpiral optimization algorithmTabu searchSoftware