Continuum mechanics
A continuum model assumes that the substance of the object completely fills the space it occupies.Continuum mechanics treats the physical properties of solids and fluids independently of any particular coordinate system in which they are observed.This permits definition of physical properties at any point in the continuum, according to mathematically convenient continuous functions.The concept of a continuum underlies the mathematical framework for studying large-scale forces and deformations in materials.A continuum is a body that can be continually sub-divided into infinitesimal elements with local material properties defined at any particular point.Properties of the bulk material can therefore be described by continuous functions, and their evolution can be studied using the mathematics of calculus.In these cases, computational methods are often used to solve the differential equations describing the evolution of material properties.An additional area of continuum mechanics comprises elastomeric foams, which exhibit a curious hyperbolic stress-strain relationship.[2] Continuum mechanics models begin by assigning a region in three-dimensional Euclidean space to the material body[citation needed] The distribution of internal contact forces throughout the volume of the body is assumed to be continuous.of a particular material point, but also on the local orientation of the surface element as defined by its normal vectorBoth are important in the analysis of stress for a polarized dielectric solid under the action of an electric field, materials where the molecular structure is taken into consideration (e.g. bones), solids under the action of an external magnetic field, and the dislocation theory of metals.In the classical branches of continuum mechanics the development of the theory of stresses is based on non-polar materials.A rigid-body displacement consists of a simultaneous translation and rotation of the body without changing its shape or size.When analyzing the motion or deformation of solids, or the flow of fluids, it is necessary to describe the sequence or evolution of configurations throughout time.In the Lagrangian description the position and physical properties of the particles are described in terms of the material or referential coordinates and time., i.e. thermodynamic properties and flow velocity, which describe or characterize features of the material body, are expressed as continuous functions of position and time, i.e.It can be thought as the rate at which the property changes when measured by an observer traveling with that group of particles.[14] Mathematically, the motion of a continuum using the Eulerian description is expressed by the mapping function which provides a tracing of the particle which now occupies the position, using the chain rule, is then The first term on the right-hand side of this equation gives the local rate of change of the propertyAll physical quantities are defined this way at each instant of time, in the current configuration, as a function of the vector positionis then given by Knowing that then It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results inThus, we have or in terms of the spatial coordinates as Continuum mechanics deals with the behavior of materials that can be approximated as continuous for certain length and time scales.The equations that govern the mechanics of such materials include the balance laws for mass, momentum, and energy.Physical restrictions on the form of the constitutive relations can be applied by requiring that the second law of thermodynamics be satisfied under all conditions.The balance laws express the idea that the rate of change of a quantity (mass, momentum, energy) in a volume must arise from three causes: LetWith respect to the reference configuration (the Lagrangian point of view), the balance laws can be written as In the above,which is the transpose of the first Piola-Kirchhoff stress tensor such that Then the balance laws become The operators in the above equations are defined as whereMore specifically, the continuum hypothesis hinges on the concepts of a representative elementary volume and separation of scales based on the Hill–Mandel condition.This condition provides a link between an experimentalist's and a theoretician's viewpoint on constitutive equations (linear and nonlinear elastic/inelastic or coupled fields) as well as a way of spatial and statistical averaging of the microstructure.
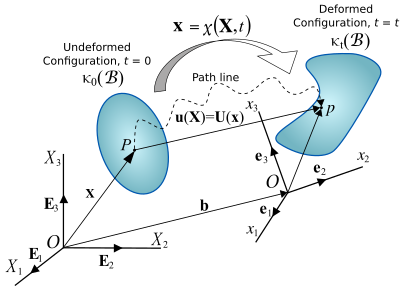
Fick's laws of diffusionMomentumEnergyClausius–Duhem (entropy)Solid mechanicsDeformationElasticitylinearPlasticityHooke's lawStressStrainFinite strainInfinitesimal strainCompatibilityBendingContact mechanicsfrictionalMaterial failure theoryFracture mechanicsFluid mechanicsFluidsStaticsDynamicsArchimedes' principleBernoulli's principleNavier–Stokes equationsPoiseuille equationPascal's lawViscosityNewtoniannon-NewtonianBuoyancyMixingPressureLiquidsAdhesionCapillary actionChromatographyCohesion (chemistry)Surface tensionAtmosphereBoyle's lawCharles's lawCombined gas lawFick's lawGay-Lussac's lawGraham's lawPlasmaRheologyViscoelasticityRheometryRheometerSmart fluidsElectrorheologicalMagnetorheologicalFerrofluidsBernoulliCauchyCharlesGay-LussacGrahamNewtonNavierPascalStokesTruesdellmechanicsforcesmaterialsdiscrete particlesrigid bodiesphysical lawsconstitutive relationshipscoordinate systemtensorscontinuous functionscrystallographic defectsinfinitesimalcalculushomogeneityisotropydifferential equationsstressesNon-Newtonian fluidNewtonian fluidselastomeric foamsEuclidean spacevectorcoordinate vectorsframe of referencefunctioncontinuousinvertibleorientation-preservingtwice continuously differentiableStress (mechanics)Cauchy stress tensorSurface forcesEuler-Cauchy's stress principleNewton's third law of motionlinear momentumangular momentumEuler's equations of motionconstitutive equationssurface integralmetallicvan der Waals forcesBody forcesgravitational fieldgravitational forceselectromagnetic forcesinertial forceselectric chargetorquesdisplacementd'Alembertfluid flowJacobian matrixDisplacement field (mechanics)displacement vectorKronecker deltasKinematicsecond law of thermodynamicsClausius–DuhemEulerian