De Broglie–Bohm theory
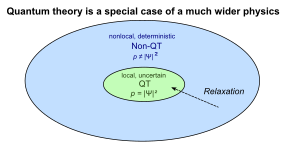
The de Broglie–Bohm theory[a] is an interpretation of quantum mechanics which postulates that, in addition to the wavefunction, an actual configuration of particles exists, even when unobserved.In Bohm's 1952 papers he used the wavefunction to construct a quantum potential that, when included in Newton's equations, gave the trajectories of the particles streaming through the two slits.[5] At every moment of time there exists not only a wavefunction, but also a well-defined configuration of the whole universe (i.e., the system as defined by the boundary conditions used in solving the Schrödinger equation).[7] Also, unlike in classical mechanics, physical properties (e.g., mass, charge) are spread out over the wavefunction in de Broglie–Bohm theory, not localized at the position of the particle.The authors then prove that the vast majority of possible initial configurations will give rise to statistics obeying the Born rule (i.e.,A low-entropy initial condition will, with overwhelmingly high probability, evolve into a higher-entropy state: behavior consistent with the second law of thermodynamics is typical.Similarly in the de Broglie–Bohm theory, there are anomalous initial conditions that would produce measurement statistics in violation of the Born rule (conflicting the predictions of standard quantum theory), but the typicality theorem shows that absent some specific reason to believe one of those special initial conditions was in fact realized, the Born rule behavior is what one should expect.[17] A renewed interest in constructing Lorentz-invariant extensions of Bohmian theory arose in the 1990s; see Bohm and Hiley: The Undivided Universe[18][19] and references therein.Initially, it had been considered impossible to set out a description of photon trajectories in the de Broglie–Bohm theory in view of the difficulties of describing bosons relativistically.[27] Chris Dewdney and G. Horton have proposed a relativistically covariant, wave-functional formulation of Bohm's quantum field theory[28][29] and have extended it to a form that allows the inclusion of gravity.It draws on Yakir Aharonov's retrocasual weak measurements to explain many-particle entanglement in a special relativistic way without the need for configuration space.The basic idea was already published by Olivier Costa de Beauregard in the 1950s and is also used by John Cramer in his transactional interpretation except the beables that exist between the von Neumann strong projection operator measurements.where Stochastic electrodynamics (SED) is an extension of the de Broglie–Bohm interpretation of quantum mechanics, with the electromagnetic zero-point field (ZPF) playing a central role as the guiding pilot-wave.Modern approaches to SED, like those proposed by the group around late Gerhard Grössing, among others, consider wave and particle-like quantum effects as well-coordinated emergent systems.To extend de Broglie–Bohm theory to curved space (Riemannian manifolds in mathematical parlance), one simply notes that all of the elements of these equations make sense, such as gradients and Laplacians.But while standard quantum mechanics is limited to discussing the results of "measurements", de Broglie–Bohm theory governs the dynamics of a system without the intervention of outside observers (p. 117 in Bell[52]).In the Einstein–Podolsky–Rosen paradox, the authors describe a thought experiment that one could perform on a pair of particles that have interacted, the results of which they interpreted as indicating that quantum mechanics is an incomplete theory.Work by Robert E. Wyatt in the early 2000s attempted to use the Bohm "particles" as an adaptive mesh that follows the actual trajectory of a quantum state in time and space.This approach has been adapted, extended, and used by a number of researchers in the chemical physics community as a way to compute semi-classical and quasi-classical molecular dynamics.[clarification needed] At the end of the presentation, Wolfgang Pauli pointed out that it was not compatible with a semi-classical technique Fermi had previously adopted in the case of inelastic scattering.An analysis of de Broglie's presentation is given in Bacciagaluppi et al.[clarification needed][87][88] Also, in 1932 John von Neumann published a no hidden variables proof in his book Mathematical Foundations of Quantum Mechanics,[89] that was widely believed to prove that all hidden-variable theories are impossible.In 1926, Erwin Madelung had developed a hydrodynamic version of Schrödinger's equation, which is incorrectly[citation needed] considered as a basis for the density current derivation of the de Broglie–Bohm theory.After publishing his popular textbook Quantum Theory that adhered entirely to the Copenhagen orthodoxy, Bohm was persuaded by Einstein to take a critical look at von Neumann's no hidden variables proof.Bohm originally hoped that hidden variables could provide a local, causal, objective description that would resolve or eliminate many of the paradoxes of quantum mechanics, such as Schrödinger's cat, the measurement problem and the collapse of the wavefunction.[96] Wolfgang Pauli, who had been unconvinced by de Broglie in 1927, conceded to Bohm as follows: I just received your long letter of 20th November, and I also have studied more thoroughly the details of your paper."[60] Bohmian mechanics is the same theory, but with an emphasis on the notion of current flow, which is determined on the basis of the quantum equilibrium hypothesis that the probability follows the Born rule.Recent studies have used this formalism to compute the evolution of many-body quantum systems, with a considerable increase in speed as compared to other quantum-based methods.[106] William Simpson has suggested a hylomorphic interpretation of Bohmian mechanics, in which the cosmos is an Aristotelian substance composed of material particles and a substantial form.Hydrodynamic pilot-wave analogs have been claimed to duplicate the double slit experiment, tunneling, quantized orbits, and numerous other quantum phenomena which have led to a resurgence in interest in pilot wave theories.[114][115] High precision measurements in the tunneling case point to a different origin of the unpredictable crossing: rather than initial position uncertainty or environmental noise, interactions at the barrier seem to be involved.
Quantum mechanicsSchrödinger equationIntroductionGlossaryHistoryClassical mechanicsOld quantum theoryBra–ket notationHamiltonianInterferenceComplementarityDecoherenceEntanglementEnergy levelMeasurementNonlocalityQuantum numberSuperpositionSymmetryTunnellingUncertaintyWave functionCollapseBell's inequalityCHSH inequalityDavisson–GermerDouble-slitElitzur–VaidmanFranck–HertzLeggett inequalityLeggett–Garg inequalityMach–ZehnderPopperQuantum eraserDelayed-choiceSchrödinger's catStern–GerlachWheeler's delayed-choiceOverviewHeisenbergInteractionMatrixPhase-spaceSchrödingerSum-over-histories (path integral)Klein–GordonRydbergInterpretationsBayesianConsistent historiesCopenhagenEnsembleHidden-variableSuperdeterminismMany-worldsObjective-collapseQuantum logicRelationalTransactionalVon Neumann–WignerRelativistic quantum mechanicsQuantum field theoryQuantum information scienceQuantum computingQuantum chaosEPR paradoxDensity matrixScattering theoryQuantum statistical mechanicsQuantum machine learningAharonovBlackettde BroglieComptonDavissonEhrenfestEinsteinEverettFeynmanGlauberGutzwillerHilbertJordanKramersLandauMoseleyMillikanPlanckSimmonsSommerfeldvon NeumannWignerZeemanZeilingerinterpretationwavefunctionLouis de BroglieDavid Bohmdeterministicnonlocalmeasurement problemBorn rulequantum equilibrium hypothesisprobability currentmomentum operatorSchrödinger's equationquantum non-equilibriumweak measurementsdouble-slit experimentwave–particle dualityquantum potential configuration spaceinitial conditionsentropysecond law of thermodynamicstheorempostulateprobability densitysquare modulusconditional probability densityspecial relativityDirac equationLorentz-invariantfoliationPartha GhoseDuffin–Kemmer–Petiau equation