Subderivative
In mathematics, subderivatives (or subgradient) generalizes the derivative to convex functions which are not necessarily differentiable.The set of subderivatives at a point is called the subdifferential at that point.[1] Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization.be a real-valued convex function defined on an open interval of the real line.Such a function need not be differentiable at all points: For example, the absolute value functionin blue has non-differentiable kinks similar to the absolute value function), for anyin the domain of the function one can draw a line which goes through the pointand which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative.Rigorously, a subderivative of a convex functionBy the converse of the mean value theorem, the set of subderivatives atfor a convex function is a nonempty closed intervalare the one-sided limitsof all subderivatives is called the subdifferential of the functionis convex, then its subdifferential at any point is non-empty.Then, the subdifferential at the origin is the intervalThe subdifferential at any pointis the singleton set, while the subdifferential at any pointThis is similar to the sign function, but is not single-valued atThe concepts of subderivative and subdifferential can be generalized to functions of several variables.is a real-valued convex function defined on a convex open set in the Euclidean spacein that space is called a subgradient atThe subdifferential is always a nonempty convex compact set.These concepts generalize further to convex functionson a convex set in a locally convex spaceThe subdifferential is always a convex closed set.It can be an empty set; consider for example an unbounded operator, which is convex, but has no subgradient.is continuous, the subdifferential is nonempty.The subdifferential on convex functions was introduced by Jean Jacques Moreau and R. Tyrrell Rockafellar in the early 1960s.The generalized subdifferential for nonconvex functions was introduced by Francis H. Clarke and R. Tyrrell Rockafellar in the early 1980s.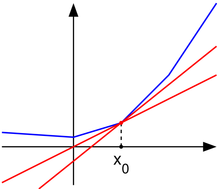
mathematicsderivativedifferentiableconvex analysisconvex functionsconvex optimizationopen intervalabsolute valuemean value theoremnonemptyclosed intervalone-sided limitsintervalsingleton setsign functionif and only ifglobal minimumMinkowski sumconvexopen setEuclidean spacedot productcompact setconvex setlocally convex spacedual spaceclosed setunbounded operatorJean Jacques MoreauR. Tyrrell RockafellarFrancis H. ClarkeWeak derivativeSubgradient methodClarke generalized derivativeRockafellar, R. T.John Wiley & SonsLemaréchal, ClaudeStack Exchange
