Convex analysis
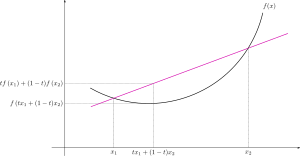
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory.is convex if it satisfies any of the following equivalent conditions: Throughout,will be a map valued in the extended real numbersthat is a convex subset of some vector space.is a convex function if holds for any realis called strictly convex.[2] The epigraphs of extended real-valued functions play a role in convex analysis that is analogous to the role played by graphs of real-valued function in real analysis.Specifically, the epigraph of an extended real-valued function provides geometric intuition that can be used to help formula or prove conjectures.while its effective domain is the set[2] The function[2] Alternatively, this means that there exists someIn words, a function is proper if its domain is not empty, it never takes on the valueis a proper convex function then there exist some vectordenotes the dot product of these vectors.The convex conjugate of an extended real-valued function(not necessarily convex) is the functionfrom the (continuous) dual spacethen the subdifferential set is For example, in the important special case whereis directly related to the convex conjugateThe biconjugate is useful for showing when strong or weak duality hold (via the perturbation function).is convex and lower semi-continuous by Fenchel–Moreau theorem.[3][4] A convex minimization (primal) problem is one of the form In optimization theory, the duality principle states that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem.In general given two dual pairs separated locally convex spaceswe can define the primal problem as findingsuch that If there are constraint conditions, these can be built into the function[5] The dual problem with respect to the chosen perturbation function is given by whereis the convex conjugate in both variables ofThe duality gap is the difference of the right and left hand sides of the inequality[6][5][7] This principle is the same as weak duality.If the two sides are equal to each other, then the problem is said to satisfy strong duality.There are many conditions for strong duality to hold such as: For a convex minimization problem with inequality constraints, the Lagrangian dual problem is where the objective functionis the Lagrange dual function defined as follows:


mathematicsconvex functionsconvex setsconvex minimizationoptimization theoryConvex setvector spaceConvex functionextended real numbersdomainepigraphgraphsreal analysiseffective domainproperproper convex functiondot productConvex conjugate(continuous) dual spacecanonical dualitystrongweak dualityperturbation functionproper functionsif and only iflower semi-continuousFenchel–Moreau theoremConvex optimizationDuality (optimization)dual pairsseparatedlocally convex spacesindicator functionduality gapstrong dualitybiconjugatelinear optimization problemSlater's conditionconvex optimization problemConvexity in economicsNon-convexity (economics)List of convexity topicsWerner FenchelRockafellar, R. Tyrrelldual normSpringer Science & Business MediaBoyd, StephenCambridge University PressLemaréchal, C.Kutateladze, Semen SamsonovichWets, Roger J.-B.Rudin, WalterMcGraw-Hill Science/Engineering/MathWorld Scientific PublishingInternet Archivevariational analysisConvex combinationTopics (list)Choquet theoryConvex geometryConvex metric spaceDualityLagrange multiplierLegendre transformationLocally convex topological vector spaceSimplexConcaveClosedLogarithmicallyPseudo-Quasi-Invex functionSemi-continuitySubderivativeCarathéodory's theoremEkeland's variational principleFenchel-Young inequalityJensen's inequalityHermite–Hadamard inequalityKrein–Milman theoremMazur's lemmaShapley–Folkman lemmaUrsescuConvex hullOrthogonallyHypographJohn ellipsoidRadial setAlgebraic interiorZonotopeDual system
