Partial derivative
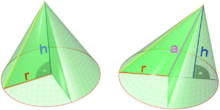
is variously denoted by It can be thought of as the rate of change of the function in theOne of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770,[1] who used it for partial differences.The modern partial derivative notation was created by Adrien-Marie Legendre (1786), although he later abandoned it; Carl Gustav Jacob Jacobi reintroduced the symbol in 1841.If all mixed second order partial derivatives are continuous at a point (or on a set), f is termed a C2 function at that point (or on that set); in this case, the partial derivatives can be exchanged by Clairaut's theorem:In fields such as statistical mechanics, the partial derivative of f with respect to x, holding y and z constant, is often expressed asIn such a case, evaluation of the function must be expressed in an unwieldy manner asThus, in these cases, it may be preferable to use the Euler differential operator notation withas the partial derivative symbol with respect to the i-th variable.as long as comparatively mild regularity conditions on f are satisfied.A common abuse of notation is to define the del operator (∇) as follows in three-dimensional Euclidean spaceThe graph of this function defines a surface in Euclidean space.To every point on this surface, there are an infinite number of tangent lines.Partial differentiation is the act of choosing one of these lines and finding its slope.To find the slope of the line tangent to the function at P(1, 1) and parallel to the xz-plane, we treat y as a constant.In this section the subscript notation fy denotes a function contingent on a fixed value of y, and not a partial derivative.Once a value of y is chosen, say a, then f(x,y) determines a function fa which traces a curve x2 + ax + a2 on the xz-plane:Own and cross partial derivatives appear in the Hessian matrix which is used in the second order conditions in optimization problems.which represents the rate with which a cone's volume changes if its radius is varied and its height is kept constant., which represents the rate with which the volume changes if its height is varied and its radius is kept constant.If (for some arbitrary reason) the cone's proportions have to stay the same, and the height and radius are in a fixed ratio k,The total derivative with respect to both r and h of the volume intended as scalar function of these two variables is given by the gradient vectorPartial derivatives appear in any calculus-based optimization problem with more than one choice variable.For example, in economics a firm may wish to maximize profit π(x, y) with respect to the choice of the quantities x and y of two different types of output.Since both partial derivatives πx and πy will generally themselves be functions of both arguments x and y, these two first order conditions form a system of two equations in two unknowns.The variables being held constant in partial derivatives here can be ratios of simple variables like mole fractions xi in the following example involving the Gibbs energies in a ternary mixture system:Ratios X, Y, Z of mole fractions can be written for ternary and multicomponent systems:This equality can be rearranged to have differential quotient of mole fractions on one side.Partial derivatives are key to target-aware image resizing algorithms.The algorithm then progressively removes rows or columns with the lowest energy.For example, a societal consumption function may describe the amount spent on consumer goods as depending on both income and wealth; the marginal propensity to consume is then the partial derivative of the consumption function with respect to income.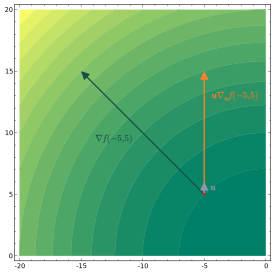
CalculusFundamental theoremLimitsContinuityRolle's theoremMean value theoremInverse function theoremDifferentialDerivativegeneralizationsinfinitesimalof a functionDifferentiation notationSecond derivativeImplicit differentiationLogarithmic differentiationRelated ratesTaylor's theoremRules and identitiesProductQuotientL'Hôpital's ruleInverseGeneral LeibnizFaà di Bruno's formulaReynoldsIntegralLists of integralsIntegral transformLeibniz integral ruleAntiderivativeimproperRiemann integralLebesgue integrationContour integrationIntegral of inverse functionsCylindrical shellsSubstitutiontrigonometrictangent half-angleEuler's formulaPartial fractionsHeaviside's methodChanging orderReduction formulaeRisch algorithmSeriesGeometricarithmetico-geometricHarmonicAlternatingBinomialTaylorConvergence testsSummand limit (term test)Direct comparisonLimit comparisonAlternating seriesCauchy condensationDirichletVectorGradientDivergenceLaplacianDirectional derivativeIdentitiesGreen'sStokes'generalized StokesHelmholtz decompositionMultivariableMatrixTensorExteriorMultiple integralLine integralSurface integralVolume integralJacobianHessianCalculus on Euclidean spaceGeneralized functionsLimit of distributionsFractionalMalliavinStochasticVariationsPrecalculusHistoryGlossaryList of topicsIntegration BeeMathematical analysisNonstandard analysismathematicstotal derivativevector calculusdifferential geometryMarquis de Condorcetpartial differencesAdrien-Marie LegendreCarl Gustav Jacob Jacobiopen subsetunit vectorcontinuousneighborhoodtotally differentiablemixed derivativesstatistical mechanicsconflatedClairaut's theoremscalar-valued functionvector fieldabuse of notationdel operatorEuclidean spaceunit vectorscontour plotscalar functionfunctiontangentsurfacetangent linespartial derivative symbolSchwarz's theoremHessian matrix

