Sign (mathematics)

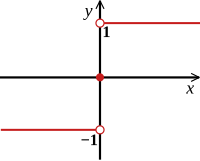
In mathematics, the sign of a real number is its property of being either positive, negative, or 0.In some contexts, it makes sense to distinguish between a positive and a negative zero.In mathematics and physics, the phrase "change of sign" is associated with exchanging an object for its additive inverse (multiplication with −1, negation), an operation which is not restricted to real numbers.It applies among other objects to vectors, matrices, and complex numbers, which are not prescribed to be only either positive, negative, or zero.This attribute of a number, being exclusively either zero (0), positive (+), or negative (−), is called its sign, and is often encoded to the real numbers 0, 1, and −1, respectively (similar to the way the sign function is defined).When a minus sign is used in between two numbers, it represents the binary operation of subtraction.When a minus sign is written before a single number, it represents the unary operation of yielding the additive inverse (sometimes called negation) of the operand.Abstractly then, the difference of two number is the sum of the minuend with the additive inverse of the subtrahend.The plus sign is predominantly used in algebra to denote the binary operation of addition, and only rarely to emphasize the positivity of an expression.Without specific context (or when no explicit sign is given), a number is interpreted per default as positive.Within the convention of zero being neither positive nor negative, a specific sign-value 0 may be assigned to the number value 0.In certain European countries, e.g. in Belgium and France, 0 is considered to be both positive and negative following the convention set forth by Nicolas Bourbaki.This notation refers to the behaviour of a function as its real input variable approaches 0 along positive (resp., negative) values; the two limits need not exist or agree.They do, however, share an attribute with the reals, which is called absolute value or magnitude.It is immediate that the quotient of any non-zero real number by its magnitude yields exactly its sign.By analogy, the sign of a complex number z can be defined as the quotient of z and its magnitude |z|.The sign of a complex number is the exponential of the product of its argument with the imaginary unit.This is accomplished by functions that extract the sign of any number, and map it to a predefined value before making it available for further calculations.For example, it might be advantageous to formulate an intricate algorithm for positive values only, and take care of the sign only afterwards.The complex sign function requires the magnitude of its argument z = x + iy, which can be calculated asExtension of sign() or signum() to any number of dimensions is obvious, but this has already been defined as normalizing a vector.In situations where there are exactly two possibilities on equal footing for an attribute, these are often labelled by convention as plus and minus, respectively.In some contexts, the choice of this assignment (i.e., which range of values is considered positive and which negative) is natural, whereas in other contexts, the choice is arbitrary, making an explicit sign convention necessary, the only requirement being consistent use of the convention.When studying one-dimensional displacements and motions in analytic geometry and physics, it is common to label the two possible directions as positive and negative.In contrast, real numbers are stored and manipulated as floating point values.Given this separate sign bit, it is possible to represent both positive and negative zero.