Space (mathematics)
In ancient Greek mathematics, "space" was a geometric abstraction of the three-dimensional reality observed in everyday life.Non-Euclidean hyperbolic geometry, introduced by Nikolai Lobachevsky in 1829 and János Bolyai in 1832 (and Carl Friedrich Gauss in 1816, unpublished)[4]: 133 stated that the sum depends on the triangle and is always less than 180 degrees.Eugenio Beltrami in 1868 and Felix Klein in 1871 obtained Euclidean "models" of the non-Euclidean hyperbolic geometry, and thereby completely justified this theory as a logical possibility.According to Bourbaki,[4]: 131 the period between 1795 (Géométrie descriptive of Monge) and 1872 (the "Erlangen programme" of Klein) can be called "the golden age of geometry".According to Bourbaki,[4]: 138 "passed over in its role as an autonomous and living science, classical geometry is thus transfigured into a universal language of contemporary mathematics".[4]: 140 Contemporary mathematicians follow this idea routinely and find it extremely suggestive to use the terminology of classical geometry nearly everywhere.A similar idea occurs in mathematical logic: a theory is called categorical if all its models of the same cardinality are mutually isomorphic.A solid arrow denotes a prevalent, so-called "canonical" transition that suggests itself naturally and is widely used, often implicitly, by default.However, it is impossible to define orthogonal (perpendicular) lines, or to single out circles among ellipses, because in a linear space there is no structure like a scalar product that could be used for measuring angles.Open sets, given in a topological space by definition, lead to such notions as continuous functions, paths, maps; convergent sequences, limits; interior, boundary, exterior.However, uniform continuity, bounded sets, Cauchy sequences, differentiable functions (paths, maps) remain undefined.Defined this way, affine and projective spaces are of algebraic nature; they can be real, complex, and more generally, over any field.The theoretical study of calculus, known as mathematical analysis, led in the early 20th century to the consideration of linear spaces of real-valued or complex-valued functions.With the operation of pointwise multiplication, it becomes a special type of Banach space, one now called a commutative von Neumann algebra.A type II von Neumann algebra determined a geometry with the peculiar feature that the dimension could be any non-negative real number, not just an integer.A slightly different approach to the geometry of function spaces developed at the same time as von Neumann and Murray's work on the classification of factors.However, the example of an irrational rotation shows that this topological space can be inaccessible to the techniques of classical measure theory.Prior to the 1940s, algebraic geometry worked exclusively over the complex numbers, and the most fundamental variety was projective space.The geometry of projective space is closely related to the theory of perspective, and its algebra is described by homogeneous polynomials.André Weil saw that geometric reasoning could sometimes be applied in number-theoretic situations where the spaces in question might be discrete or even finite.One of the motivations for scheme theory is that polynomials are unusually structured among functions, and algebraic varieties are consequently rigid.The topological space and the structure sheaf together are required to satisfy conditions that mean the functions come from algebraic operations.These two operations are mutually inverse, so affine schemes provide a new language with which to study questions in commutative algebra.DM stacks are similar to schemes, but they permit singularities that cannot be described solely in terms of polynomials.For example, the quotient of the affine plane by a finite group of rotations around the origin yields a Deligne–Mumford stack that is not a scheme or an algebraic space.Away from the origin, the quotient by the group action identifies finite sets of equally spaced points on a circle.A topological space (in the ordinary sense) axiomatizes the notion of "nearness," making two points be nearby if and only if they lie in many of the same open sets.A locale is defined to be a complete Heyting algebra, and the elementary properties of topological spaces are re-expressed and reproved in these terms.According to Kevin Arlin, Nevertheless, a general definition of "structure" was proposed by Bourbaki;[2] it embraces all types of spaces mentioned above, (nearly?)Many mathematical structures of geometric flavor treated in the "Non-commutative geometry", "Schemes" and "Topoi" subsections above do not stipulate a base set of points.

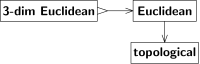
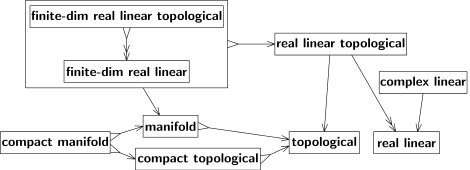





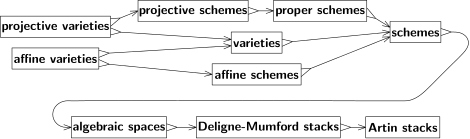

Space (disambiguation)mathematicsuniversestructureelementssubsetEuclidean spaceslinear spacestopological spacesHilbert spacesprobability spacesmathematical objectspointsisomorphismgeometric "space"algebraic "structure"BourbakiHistory of geometryEuclidanalytic geometryRené Descartesequivalence relationscongruencesimilarityhomothetiesGaspard Mongeprojective geometryhyperbolic geometryNikolai LobachevskyJános BolyaiCarl Friedrich GaussEugenio BeltramiFelix Kleinnon-Euclidean geometry"Erlangen programme"Euclidean spaceHilbert's axiomsTarski's axiomsBirkhoff's axiomsprimitive notionsaxiomsDedekind cutsprojective spaceBernhard RiemannFunctionsfunction spacesfunctional analysisprojective spaceshomeomorphismcategory theoryforgetfulfunctorclassesself-homeomorphisminjectivesurjectivebijectiveinversecommutativefine topologyalgebraicreal numberscomplex numberscomplex planelinearly independentanalyticOpen setscontinuous functionsconvergent sequences, limitsuniform continuitybounded setsCauchy sequencesdifferentiable functionsopen intervalreal lineclosed intervalinductive dimensionLebesgue covering dimensiongeneral topologyCompact topological spacesextended real linemanifoldslinear topological spaceaffineJohn Baezmetric spacemetrizablecompleteHausdorff dimensionfractalsUniform spacesnormed spaceBanach spaceinner product spaceHilbert spacequantum theorySmooth manifoldsRiemannian manifoldpseudo-Riemann spacesgeneral relativitymeasure theoryAndrey Kolmogorov'sprobability theorymeasurable setsmeasurable spaceσ-algebra.Borel setsBaire setsuniversally measurable setsnorm topologyweak topologyseparablestandard Borel spacesmeasure spaceLebesgue measureIntegration theoryprobability spaceGaussian measuresStandard probability spacesdisintegration of measuremathematical analysisBanach algebrasvon Neumann algebraJohn von NeumannFrancis Murraydirect integral