Complex analysis
It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory.Complex analysis is one of the classical branches in mathematics, with roots in the 18th century and just prior.Important mathematicians associated with complex numbers include Euler, Gauss, Riemann, Cauchy, Gösta Mittag-Leffler, Weierstrass, and many more in the 20th century.In modern times, it has become very popular through a new boost from complex dynamics and the pictures of fractals produced by iterating holomorphic functions.In particular, every differentiable complex function is analytic (see next section), and two differentiable functions that are equal in a neighborhood of a point are equal on the intersection of their domain (if the domains are connected).Complex functions that are differentiable at every point of an open subsetis defined to be[2] Superficially, this definition is formally analogous to that of the derivative of a real function.However, complex derivatives and differentiable functions behave in significantly different ways compared to their real counterparts.For instance, holomorphic functions are infinitely differentiable, whereas the existence of the nth derivative need not imply the existence of the (n + 1)th derivative for real functions.are not holomorphic anywhere on the complex plane, as can be shown by their failure to satisfy the Cauchy–Riemann conditions (see below).An important property of holomorphic functions is the relationship between the partial derivatives of their real and imaginary components, known as the Cauchy–Riemann conditions., In terms of the real and imaginary parts of the function, u and v, this is equivalent to the pair of equationsFor instance, Picard's theorem asserts that the range of an entire function can take only three possible forms:In mathematics, a conformal map is a function that locally preserves angles, but not necessarily lengths.Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature.The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation.The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (orthogonal with determinant one).Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix.In three and higher dimensions, Liouville's theorem sharply limits the conformal mappings to a few types.One of the central tools in complex analysis is the line integral.The line integral around a closed path of a function that is holomorphic everywhere inside the area bounded by the closed path is always zero, as is stated by the Cauchy integral theorem.The values of such a holomorphic function inside a disk can be computed by a path integral on the disk's boundary (as shown in Cauchy's integral formula).The remarkable behavior of holomorphic functions near essential singularities is described by Picard's theorem.Functions that have only poles but no essential singularities are called meromorphic.Laurent series are the complex-valued equivalent to Taylor series, but can be used to study the behavior of functions near singularities through infinite sums of more well understood functions, such as polynomials.A bounded function that is holomorphic in the entire complex plane must be constant; this is Liouville's theorem.This allows the extension of the definition of functions, such as the Riemann zeta function, which are initially defined in terms of infinite sums that converge only on limited domains to almost the entire complex plane.Sometimes, as in the case of the natural logarithm, it is impossible to analytically continue a holomorphic function to a non-simply connected domain in the complex plane but it is possible to extend it to a holomorphic function on a closely related surface known as a Riemann surface.The Riemann mapping theorem about the conformal relationship of certain domains in the complex plane, which may be the most important result in the one-dimensional theory, fails dramatically in higher dimensions.A major application of certain complex spaces is in quantum mechanics as wave functions.


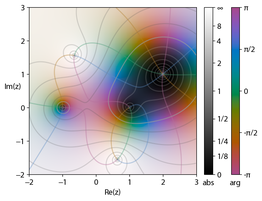
Hue represents the argument , brightness the magnitude.
Complexity theoryMathematical analysisComplex numbersReal numberImaginary numberComplex planeComplex conjugateUnit complex numberAnalytic functionHolomorphic functionCauchy–Riemann equationsFormal power seriesZeros and polesCauchy's integral theoremLocal primitiveCauchy's integral formulaWinding numberLaurent seriesIsolated singularityResidue theoremArgument principleConformal mapSchwarz lemmaHarmonic functionLaplace's equationLiouville's theoremPicard theoremGeometric function theoryAugustin-Louis CauchyLeonhard EulerCarl Friedrich GaussJacques HadamardKiyoshi OkaBernhard RiemannKarl Weierstrassfunctionsalgebraic geometrynumber theoryanalytic combinatoricsapplied mathematicsphysicshydrodynamicsthermodynamicsquantum mechanicstwistor theorynuclearaerospacemechanicalelectrical engineeringdifferentiable functionsum functionTaylor seriesanalyticanalytic functionsholomorphic functionsfunctions of several complex variablesRiemannCauchyGösta Mittag-LefflerWeierstrassconformal mappingsanalytic number theorycomplex dynamicsfractalsstring theoryquantum field theoryexponentialintegergeometric progressionfunctiondomaincodomainopen subsetimaginaryisomorphicordered pairreal-valued functionsvector-valued functioncontinuitydifferentiabilitydifferentiable complex functionneighborhoodconnectedanalytic continuationcurve arcsspecialcomplex logarithm functionsdifferentiableinfinitely differentiableanalyticityexponential functiontrigonometric functionspolynomial functionsCauchy–Riemann conditionsregionLooman–Menchoff theoremPicard's theoremmathematicsanglescurvescurvatureJacobiancoordinate transformationrotation matrixorthogonalcomplex analyticRiemanniansemi-Riemannian manifoldsColor wheel graphargumentbrightnessline integralCauchy integral theoremresiduesmethods of contour integrationessential singularitiesmeromorphicbounded functionfundamental theorem of algebraalgebraically closedanalytically continuedRiemann zeta functionnatural logarithmRiemann surfacecomplex analysis in more than one complex dimensionpower series
