Fiber bundle
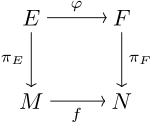
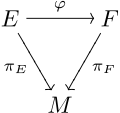
In mathematics, and particularly topology, a fiber bundle (Commonwealth English: fibre bundle) is a space that is locally a product space, but globally may have a different topological structure.Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces.Fiber bundles can be specialized in a number of ways, the most common of which is requiring that the transition maps between the local trivial patches lie in a certain topological group, known as the structure group, acting on the fiberIn topology, the terms fiber (German: Faser) and fiber space (gefaserter Raum) appeared for the first time in a paper by Herbert Seifert in 1933,[1][2][3] but his definitions are limited to a very special case.[5] The theory of fibered spaces, of which vector bundles, principal bundles, topological fibrations and fibered manifolds are a special case, is attributed to Herbert Seifert, Heinz Hopf, Jacques Feldbau,[6] Whitney, Norman Steenrod, Charles Ehresmann,[7][8][9] Jean-Pierre Serre,[10] and others.Fiber bundles became their own object of study in the period 1935–1940.is a continuous surjection satisfying a local triviality condition outlined below.carries the quotient topology determined by the mapAny fiber bundle over a contractible CW-complex is trivial.It has the circle that runs lengthwise along the center of the strip as a base, so the Möbius strip is a bundle of the line segment over the circle.in the picture is a (somewhat twisted) slice of the strip four squares wide and one long (i.e. all the points that project to(the trivializing neighborhood) to a slice of a cylinder: curved, but not twisted.This twist is visible only globally; locally the Möbius strip and the cylinder are identical (making a single vertical cut in either gives the same space).A sphere bundle is partially characterized by its Euler class, which is a degreecohomology class in the total space of the bundle.Mapping tori of homeomorphisms of surfaces are of particular importance in 3-manifold topology.The most general conditions under which the quotient map will admit local cross-sections are not known, although ifThe abelian subgroup of diagonal matrices is isomorphic to the circle groupSince bundles do not in general have globally defined sections, one of the purposes of the theory is to account for their existence.The most well-known example is the hairy ball theorem, where the Euler class is the obstruction to the tangent bundle of the 2-sphere having a nowhere vanishing section.A local section of a fiber bundle is a continuous mapFiber bundles often come with a group of symmetries that describe the matching conditions between overlapping local trivialization charts.Specifically, let G be a topological group that acts continuously on the fiber space F on the left.We lose nothing if we require G to act faithfully on F so that it may be thought of as a group of homeomorphisms of F. A G-atlas for the bundleA G-bundle is a fiber bundle with an equivalence class of G-atlases.The importance of this is that the transition functions determine the fiber bundle (if one assumes the Čech cocycle condition).A principal G-bundle is a G-bundle where the fiber F is a principal homogeneous space for the left action of G itself (equivalently, one can specify that the action of G on the fiber F is free and transitive, i.e. regular).In this case, it is often a matter of convenience to identify F with G and so obtain a (right) action of G on the principal bundle.admits a compatible fiber bundle structure (Michor 2008, §17).




optical fiber bundlehairbrushbristlesmathematicstopologyCommonwealth Englishproduct spacetopological structurecontinuoussurjectiveprojectionsubmersiontrivialMöbius stripKlein bottlecovering spacestangent bundlemanifoldvector bundlesdifferential geometrydifferential topologyprincipal bundlesbundle mapscategoryidentity mappingsectiontransition mapstopological groupHerbert SeifertHassler Whitneyfibrationsfibered manifoldsHeinz HopfJacques FeldbauNorman SteenrodCharles EhresmannJean-Pierre Serresphere bundledimensiontopological spacessurjectionconnectedneighborhoodhomeomorphismsubspace topologycommutepreimageopen mapquotient topologyshort exact sequencesmooth manifoldsfunctionssmooth mapscontractibleCW-complexcircleline segmentlengthcylinderimmersedcovering spacelocal homeomorphismdiscrete spacevector spaceslinear groupcotangent bundleframe bundletransitiveactionprincipal homogeneous spacerepresentationassociated bundlen-spheremetricRiemannian manifoldunit vectorsunit tangent bundleEuler classcohomologycircle bundleChern classlong exact sequenceGysin sequenceWang sequencetopological spacemapping torussurfaces3-manifold topologyclosed subgroupquotient spacenecessary and sufficient conditionquotient mapLie groupLie subgroupCartan's theoremHopf fibrationspecial unitary groupabeliandiagonal matricesisomorphiccircle groupdiffeomorphicSection (fiber bundle)for allobstructioncharacteristic classesalgebraic topologyhairy ball theorem2-sphereopen set1-1 correspondencefaithfullyhomeomorphismsphysicsgauge groupČech cohomologyprincipal G-bundleBundle mapcommutativemorphismsequivariantcoversisomorphismdifferentiable manifoldssubmersionsfibered manifold
