Linear map
Sometimes the term linear operator refers to this case,[1] but the term "linear operator" can have different meanings for different conventions: for example, it can be used to emphasize that(possibly of a lower dimension);[3] for example, it maps a plane through the origin inthe following two conditions are satisfied: Thus, a linear map is said to be operation preserving.In other words, it does not matter whether the linear map is applied before (the right hand sides of the above examples) or after (the left hand sides of the examples) the operations of addition and scalar multiplication.viewed as a one-dimensional vector space over itself is called a linear functional.without modification, and to any right-module upon reversing of the scalar multiplication.Indeed, the Hahn–Banach dominated extension theorem even guarantees that when this linear functionalMatrices yield examples of linear maps: ifwhich implies that the function f is entirely determined by the vectorsThis is because the values of the elements of a matrix depend on the bases chosen.The matrices of a linear transformation can be represented visually: Such that starting in the bottom left cornerIn two-dimensional space R2 linear maps are described by 2 × 2 matrices.It follows from this that the class of all vector spaces over a given field K, together with K-linear maps as morphisms, forms a category.Given again the finite-dimensional case, if bases have been chosen, then the composition of linear maps corresponds to the matrix multiplication, the addition of linear maps corresponds to the matrix addition, and the multiplication of linear maps with scalars corresponds to the multiplication of matrices with scalars.together with addition, composition and scalar multiplication as defined above forms an associative algebra with identity element over the fieldSince the automorphisms are precisely those endomorphisms which possess inverses under composition,An example illustrating the infinite-dimensional case is afforded by the map f: R∞ → R∞,), but in the infinite-dimensional case it cannot be inferred that the kernel and the co-kernel of an endomorphism have the same dimension (0 ≠ 1).Its image is the entire target space, and hence its co-kernel has dimension 0, but since it maps all sequences in which only the first element is non-zero to the zero sequence, its kernel has dimension 1.For a linear operator with finite-dimensional kernel and co-kernel, one may define index as:namely the degrees of freedom minus the number of constraints.The index of an operator is precisely the Euler characteristic of the 2-term complex 0 → V → W → 0.The following incomplete list enumerates some important classifications that do not require any additional structure on the vector space.Let V and W denote vector spaces over a field F and let T: V → W be a linear map.T is said to be injective or a monomorphism if any of the following equivalent conditions are true: T is said to be surjective or an epimorphism if any of the following equivalent conditions are true: T is said to be an isomorphism if it is both left- and right-invertible.This is equivalent to T being both one-to-one and onto (a bijection of sets) or also to T being both epic and monic, and so being a bimorphism.An example of an unbounded, hence discontinuous, linear transformation is differentiation on the space of smooth functions equipped with the supremum norm (a function with small values can have a derivative with large values, while the derivative of 0 is 0).For a specific example, sin(nx)/n converges to 0, but its derivative cos(nx) does not, so differentiation is not continuous at 0 (and by a variation of this argument, it is not continuous anywhere).A specific application of linear maps is for geometric transformations, such as those performed in computer graphics, where the translation, rotation and scaling of 2D or 3D objects is performed by the use of a transformation matrix.Linear mappings also are used as a mechanism for describing change: for example in calculus correspond to derivatives; or in relativity, used as a device to keep track of the local transformations of reference frames.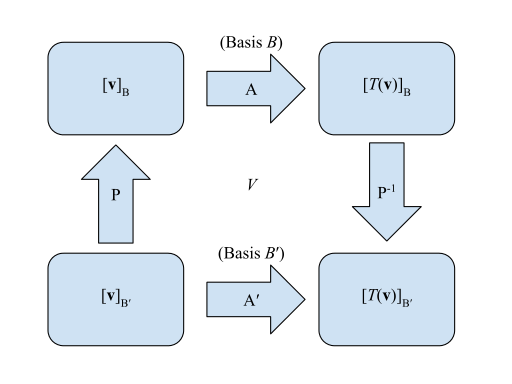
Möbius transformationLinear Operators (book)linear functionmathematicslinear algebramappingvector spacesvector additionscalar multiplicationmodulesModule homomorphismbijectionfunction spacefunctional analysisanalysislinear subspacesdimensionoriginmatricesrotation and reflection linear transformationscategory theorymorphismsequivalentthe one of matricesAdditivityHomogeneitylinear combinationslinear functionalhomothetyidentity mapaffine transformationreal matrixcolumn vectorfinite-dimensionalisometrynormed spacesDifferentiationlinear operatorsmooth functionslinear endomorphismdomaincodomainintegralintervalantiderivativequotient spacelinear isomorphismexpected valuevariancelinear spanfunctionextendsvector subspaceHahn–Banach dominated extension theoremseminormTransformation matrixmatrixEuclidean spacedimensionalrotationreflectionscalinghorizontal shear mappingsqueeze mappingprojectionconformal linear transformationcompositioncategoryinversepointwiseassociative algebracomposition of mapsmatrix multiplicationmatrix additionEndomorphismAutomorphismisomorphismautomorphism groupendomorphismsisomorphicgeneral linear groupKernel (linear algebra)Image (mathematics)Rank of a matrixkernelsubspacerank–nullity theoremCokernelexact sequencedegrees of freedomEuler characteristicoperator theoryFredholm operatorsAtiyah–Singer index theoreminjectivemonomorphismone-to-oneleft-invertiblesurjectiveepimorphismright-invertiblebimorphismnilpotentidempotentscalar matrixBasis (linear algebra)Change of basiscontravariantvarianttensorsContinuous linear operatorDiscontinuous linear maptopological vector spacescontinuousboundeddiscontinuous linear operatorsgeometric transformationscomputer graphicscompiler optimizationsparallelizing compilerAdditive mapAntilinear mapBent functionBounded operatorCauchy's functional equationLinear isometry