Hubbard model
In particular, the Hubbard term, most commonly denoted by U, is applied in first principles based simulations using Density Functional Theory, DFT.For example, the Hubbard model correctly predicts the existence of Mott insulators: materials that are insulating due to the strong repulsion between electrons, even though they satisfy the usual criteria for conductors, such as having an odd number of electrons per unit cell.[2] Since then, it has been applied to the study of high-temperature superconductivity, quantum magnetism, and charge density waves.[5] The Hubbard model is based on the tight-binding approximation from solid-state physics, which describes particles moving in a periodic potential, typically referred to as a lattice.For real materials, each lattice site might correspond with an ionic core, and the particles would be the valence electrons of these ions.The system is said to be in the tight-binding limit when the strength of the hopping integrals falls off rapidly with distance.The Hubbard model introduces a contact interaction between particles of opposite spin on each site of the lattice.For example, it has been used to describe metal oxides as they are heated, where the corresponding increase in nearest-neighbor spacing reduces the hopping integral to the point where the on-site potential is dominant.Similarly, the Hubbard model can explain the transition from conductor to insulator in systems such as rare-earth pyrochlores as the atomic number of the rare-earth metal increases, because the lattice parameter increases (or the angle between atoms can also change) as the rare-earth element atomic number increases, thus changing the relative importance of the hopping integral compared to the on-site repulsion.[2] But in the case where the spacing between the hydrogen atoms is gradually increased, at some point the chain must become an insulator.Without the contribution of the second term, the Hamiltonian resolves to the tight binding formula from regular band theory.Including the second term yields a realistic model that also predicts a transition from conductor to insulator as the ratio of interaction to hopping,The one-dimensional Hubbard model was solved by Lieb and Wu using the Bethe ansatz.Essential progress was achieved in the 1990s: a hidden symmetry was discovered, and the scattering matrix, correlation functions, thermodynamic and quantum entanglement were evaluated.However, it is possible for the electrons to exhibit another kind of behavior: This is known as charge transfer and results in charge-transfer insulators.The fact that the Hubbard model has not been solved analytically in arbitrary dimensions has led to intense research into numerical methods for these strongly correlated electron systems.[7][8] One major goal of this research is to determine the low-temperature phase diagram of this model, particularly in two-dimensions.With projector and finite-temperature auxiliary-field Monte Carlo, two statistical methods exist that can obtain certain properties of the system.This scheme maps the Hubbard Hamiltonian onto a single-site impurity model, a mapping that is formally exact only in infinite dimensions and in finite dimensions corresponds to the exact treatment of all purely local correlations only.Within DMFT, the evolution of the spectral function can be computed and the appearance of the upper and lower Hubbard bands can be observed as correlations increase.Stacks of heterogeneous 2-dimensional transition metal dichalcogenides (TMD) have been used to simulate geometries in more than one dimension.This created a moiré superlattice consisting of hexagonal supercells (repetition units defined by the relationship of the two materials).One result of the simulation showed that the difference between metal and insulator is a continuous function of the electric field strength.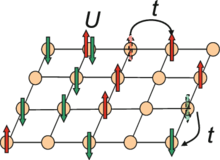
approximate modelconductinginsulating systemssolid-state physicsJohn HubbardHamiltoniantunnelingfermionsbosonsBose–Hubbard modelBloch bandDensity Functional Theorytight-binding modelMott insulatorsMartin Gutzwillerhigh-temperature superconductivitytight-bindinglatticeWannier stateseigenstatescrystallineBloch's functionsenergy bandsscreened Coulomb interactionkinetic energyrare-earthpyrochloresatomic numberlattice parameterhydrogen atomPauli exclusion principleband theorysecond quantizationtight bindingmagnetic momentssuperexchangeBethe ansatzhidden symmetryscattering matrixcorrelation functionsthermodynamicquantum entanglementMott–Hubbardcharge-transfer insulatorsLanczos algorithmauxiliary-field Monte Carlosign problemdynamical mean-field theorysingle-site impurity modelGreen's functionspectral functiontransition metal dichalcogenides (TMD)Tungsten diselenidemoirésupercellsWigner crystalsElectrodeselectric fieldoxygenanomalous quantum Hall effectKelvinsAnderson impurity modelBloch's theoremElectronic band structuret-J modelHeisenberg model (quantum)Stoner criterionCambridge University PressBibcodeProceedings of the Royal Society of LondonJournal of Statistical PhysicsSpringerPhysica AAnnual Review of Condensed Matter PhysicsCondensed matter physicsStates of matterLiquidPlasmaBose–Einstein condensateFermionic condensateFermi gasSupersolidSuperfluidLuttinger liquidTime crystalOrder parameterPhase transitionSpontaneous symmetry breakingCritical phenomenaHall effectQuantum Hall effectSpin Hall effectQuantum spin Hall effectBerry phaseAharonov–Bohm effectJosephson effectKondo effectDrude modelFree electron modelNearly free electron modelFermi liquid theoryAnderson localizationBCS theorytight binding modelInsulatorMott insulatorSemiconductorSemimetalConductorSuperconductorTopological insulatorSpin gapless semiconductorThermoelectricityPiezoelectricityFerroelectricityFlexoelectricityElectrostrictionAmorphous magnetDiamagnetSuperdiamagnetParamagnetSuperparamagnetFerromagnetAntiferromagnetMetamagnetSpin glass