Absolute magnitude
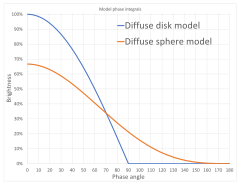
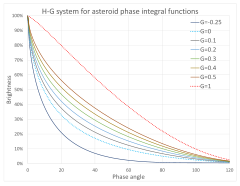
An object's absolute magnitude is defined to be equal to the apparent magnitude that the object would have if it were viewed from a distance of exactly 10 parsecs (32.6 light-years), without extinction (or dimming) of its light due to absorption by interstellar matter and cosmic dust.By hypothetically placing all objects at a standard reference distance from the observer, their luminosities can be directly compared among each other on a magnitude scale.For Solar System bodies that shine in reflected light, a different definition of absolute magnitude (H) is used, based on a standard reference distance of one astronomical unit.[3] In stellar and galactic astronomy, the standard distance is 10 parsecs (about 32.616 light-years, 308.57 petameters or 308.57 trillion kilometres).A galaxy's magnitude is defined by measuring all the light radiated over the entire object, treating that integrated brightness as the brightness of a single point-like or star-like source, and computing the magnitude of that point-like source as it would appear if observed at the standard 10 parsecs distance.Some stars visible to the naked eye have such a low absolute magnitude that they would appear bright enough to outshine the planets and cast shadows if they were at 10 parsecs from the Earth.Some active galactic nuclei (quasars like CTA-102) can reach absolute magnitudes in excess of −32, making them the most luminous persistent objects in the observable universe, although these objects can vary in brightness over astronomically short timescales.At the extreme end, the optical afterglow of the gamma ray burst GRB 080319B reached, according to one paper, an absolute r magnitude brighter than −38 for a few tens of seconds.[6] The Greek astronomer Hipparchus established a numerical scale to describe the brightness of each star appearing in the sky.Typical extinction rates within the Milky Way galaxy are 1 to 2 magnitudes per kiloparsec, when dark clouds are taken into account.Moreover, the cosmological redshift complicates the relationship between absolute and apparent magnitude, because the radiation observed was shifted into the red range of the spectrum.The Black Eye Galaxy has a visual magnitude mV of 9.36 and a distance modulus μ of 31.06:The absolute bolometric magnitude (Mbol) takes into account electromagnetic radiation at all wavelengths.It includes those unobserved due to instrumental passband, the Earth's atmospheric absorption, and extinction by interstellar dust.where In August 2015, the International Astronomical Union passed Resolution B2[9] defining the zero points of the absolute and apparent bolometric magnitude scales in SI units for power (watts) and irradiance (W/m2), respectively.Placing a radiation source (e.g. star) at the standard distance of 10 parsecs, it follows that the zero point of the apparent bolometric magnitude scale mbol = 0 corresponds to irradiance f0 = 2.518021002×10−8 W/m2.However, on this SI power scale, the nominal solar luminosity corresponds closely to Mbol = 4.74, a value that was commonly adopted by astronomers before the 2015 IAU resolution.[10] The luminosity of the star in watts can be calculated as a function of its absolute bolometric magnitude Mbol as:, is defined as the apparent magnitude that the object would have if it were one astronomical unit (AU) from both the Sun and the observer, and in conditions of ideal solar opposition (an arrangement that is impossible in practice).The absolute magnitude is the brightness at phase angle zero, an arrangement known as opposition, from a distance of one AU., which isn't realistic, but it does represent the opposition surge for rough surfaces that reflect more uniform light back at low phase angles., a measure for the reflectivity of planetary surfaces, is based on the diffuse disk reflector model.This is not a good approximation, because the phase curve of the Moon is too complicated for the diffuse reflector model.Neptune's absolute magnitude is changing slowly due to seasonal effects as the planet moves along its 165-year orbit around the Sun, and the approximation above is only valid after the year 2000.Accounting for the high phase angle, the correction term above yields an actual apparent magnitude ofDue to the variability of the weather, Earth's apparent magnitude cannot be predicted as accurately as that of most other planets.[20] If an object has an atmosphere, it reflects light more or less isotropically in all directions, and its brightness can be modelled as a diffuse reflector.called absolute magnitude and slope, to model the opposition effect for the ephemerides published by the Minor Planet Center.[30] In addition, their absolute magnitude can vary with the viewing direction, depending on their axial tilt.[43] For a meteor, the standard distance for measurement of magnitudes is at an altitude of 100 km (62 mi) at the observer's zenith.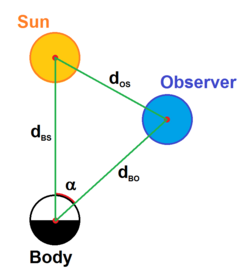



Absolute Magnitude (magazine)astronomyluminositycelestial objectlogarithmicastronomical magnitudeapparent magnitudeparsecslight-yearsextinctioninterstellar mattercosmic dustSolar Systemastronomical unitMilky WayB magnitudemagnitudeswavelengthfilterpassbandsUBV photometric systemwavelengthsbolometric correctionparallaxmilliarcsecondsextended objectsplanetsBetelgeuseSiriuselliptical galaxy M87active galactic nucleiquasarsCTA-102GRB 080319Br magnitudeHipparchuscommon logarithmextinction from gas and dustdark cloudsEuclideangeneral relativitycosmological redshiftK correctionstellar parallaxdistance modulusBlack Eye GalaxyApparent bolometric magnitudebolometricelectromagnetic radiationpassbandextinction by interstellar dusteffective temperatureInternational Astronomical Unionzero pointsbolometric magnituderadiationirradiancesolar irradiancesolar constantMagnitude (astronomy)asteroidsphase anglephase curveoppositionlaw of cosinesreflectingintegrationunit conversionroughnessideal diffuse reflectingspheresdegreesopposition surgegeometric albedokilometersMoon'squarter phaseobservations at different phase anglesAstronomical AlmanacMercuryJupiterSaturnUranusNeptuneSaturn's ringsCommon Eranear side of the Moonfirst quarter phaselast quarteralbedoaltostratus cloudweather1 Ceresopposition effectsemi-empiricalephemeridesMinor Planet Center101955 BennuJet Propulsion Laboratoryvaries as they rotaterotation periodaxial tiltcometsC/2011 L4 (PANSTARRS)Comet SarabatComet Hale-BoppComet HalleyC/2014 UN271 (Bernardinelli-Bernstein)289P/BlanpainmeteorzenithAraucaria ProjectHertzsprung–Russell diagramtemperatureJanskyList of most luminous starsPhotographic magnitudeSurface brightnessZero point (photometry)NASA Goddard Space Flight CenterBibcodeThe Astrophysical JournalSpringer Science & Business MediaThe New York TimesNASA Jet Propulsion LaboratoryWayback Machine



