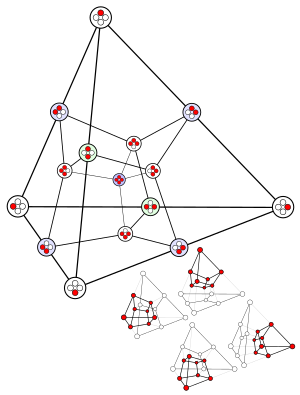
Simplex
The concept of a simplex was known to William Kingdon Clifford, who wrote about these shapes in 1886 but called them "prime confines".A fourth family, the tessellation of n-dimensional space by infinitely many hypercubes, he labeled as δn.[4] The convex hull of any nonempty subset of the n + 1 points that define an n-simplex is called a face of the simplex.In particular, the convex hull of a subset of size m + 1 (of the n + 1 defining points) is an m-simplex, called an m-face of the n-simplex.This idea can be generalized, that is, adding a single new point outside the currently occupied space, which requires going to the next higher dimension to hold the new shape.This convention is more common in applications to algebraic topology (such as simplicial homology) than to the study of polytopes.These Petrie polygons (skew orthogonal projections) show all the vertices of the regular simplex on a circle, and all vertex pairs connected by edges.Especially in numerical applications of probability theory a projection onto the standard simplex is of interest.It is also possible to directly write down a particular regular n-simplex in Rn which can then be translated, rotated, and scaled as desired.The additional vertex must lie on the line perpendicular to the barycenter of the standard simplex, so it has the form (α/n, ..., α/n) for some real number α.Solving this equation shows that there are two choices for the additional vertex: Either of these, together with the standard basis vectors, yields a regular n-simplex.A highly symmetric way to construct a regular n-simplex is to use a representation of the cyclic group Zn+1 by orthogonal matrices.Applying powers of this matrix to an appropriate vector v will produce the vertices of a regular n-simplex.A sufficient condition for the orbit of a point to be a regular simplex is that the matrices Qi form a basis for the non-trivial irreducible real representations of Zn+1, and the vector being rotated is not stabilized by any of them.For example, when n = 4, one possible matrix is Applying this to the vector (1, 0, 1, 0) results in the simplex whose vertices are each of which has distance √5 from the others.The expression employs a Gram determinant and works even when the n-simplex's vertices are in a Euclidean space with more than n dimensions, e.g., a triangle inis Another common way of computing the volume of the simplex is via the Cayley–Menger determinant, which works even when the n-simplex's vertices are in a Euclidean space with more than n dimensions.The following assertions hold: If P is the unit n-hypercube, then the union of the n-simplexes formed by the convex hull of each n-path is P, and these simplexes are congruent and pairwise non-overlapping.[12] In particular, the volume of such a simplex is If P is a general parallelotope, the same assertions hold except that it is no longer true, in dimension > 2, that the simplexes need to be pairwise congruent; yet their volumes remain equal, because the n-parallelotope is the image of the unit n-hypercube by the linear isomorphism that sends the canonical basis ofAs previously, this implies that the volume of a simplex coming from a n-path is: Conversely, given an n-simplexFinally, the formula at the beginning of this section is obtained by observing that From this formula, it follows immediately that the volume under a standard n-simplex (i.e. between the origin and the simplex in Rn+1) is The volume of a regular n-simplex with unit side length is as can be seen by multiplying the previous formula by xn+1, to get the volume under the n-simplex as a function of its vertex distance x from the origin, differentiating with respect to x, atSuch simplices are generalizations of right triangles and for them there exists an n-dimensional version of the Pythagorean theorem: The sum of the squared (n − 1)-dimensional volumes of the facets adjacent to the orthogonal corner equals the squared (n − 1)-dimensional volume of the facet opposite of the orthogonal corner.The Hasse diagram of the face lattice of an n-simplex is isomorphic to the graph of the (n + 1)-hypercube's edges, with the hypercube's vertices mapping to each of the n-simplex's elements, including the entire simplex and the null polytope as the extreme points of the lattice (mapped to two opposite vertices on the hypercube).Aitchinson geometry is a natural way to construct an inner product space from the standard simplexA finite set of k-simplexes embedded in an open subset of Rn is called an affine k-chain.Thus, an affine chain takes the symbolic form of a sum with integer coefficients.More generally, a simplex (and a chain) can be embedded into a manifold by means of smooth, differentiable mapIn this case, both the summation convention for denoting the set, and the boundary operation commute with the embedding.)[16] Since classical algebraic geometry allows one to talk about polynomial equations but not inequalities, the algebraic standard n-simplex is commonly defined as the subset of affine (n + 1)-dimensional space, where all coordinates sum up to 1 (thus leaving out the inequality part).By using the same definitions as for the classical n-simplex, the n-simplices for different dimensions n assemble into one simplicial object, while the rings

Simplex (disambiguation)geometrytriangletetrahedrondimensionspolytope0-dimensional1-dimensionalline segment2-dimensional3-dimensional4-dimensional5-cellconvex hullverticesaffinely independentlinearly independentregular polytopeunit vectorstopologycombinatoricssimplicial complexabstract simplicial complexfinite setWilliam Kingdon CliffordHenri Poincaréalgebraic topologyPieter Hendrik SchouteDonald Coxetercross-polytopehypercubestessellation of n-dimensional space by infinitely many hypercubesnonemptysubsetbinomial coefficientPascal's trianglef-vector7-simplextriangle numbertetrahedron numberSchläfliCoxeter5-simplex6-simplex8-simplex9-simplex10-simplexisosceles triangleequilateral triangleregular tetrahedronpower of twotesseractsimplicial homologyPetrie polygonscircleaffine hyperplane0/1-polytopeorthoplexbarycentric coordinatesaffine transformationorientation preservinggeneralized barycentric coordinatessoftmax functionstandard logistic functionindefinite suminteriorfundamental domainactionsymmetric groupprobability theoryprojectionmedian-findingsimplex methodbasis vectorsreal numberquadratic equationcyclic grouporthogonal matricesidentity matrixmatrixdividingintegervolumedeterminantvectorGram determinantCayley–Menger determinantpermutationlinear isomorphismdihedral anglePythagorean theoremde Gua's theoremHasse diagramhypercubevertex figureTopologicallyequivalentn-ballmanifold with cornersCategorical distributionAitchison geometryinner product spacehexagramcompound of two tetrahedrastella octangulacompound of two 5-cellstopological spacessimplicial complexescombinatorialhomologyopen subsetmultiplicityorientationboundarymanifoldembeddingmap operationcontinuous maptopological spacealgebraic geometryschemesimplicial objectcategoryK-theoryChow groupsstatistics