Scale-free network

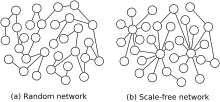
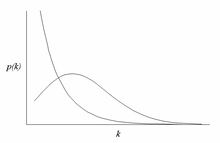
[1][2] The name "scale-free" could be explained by the fact that some moments of the degree distribution are not defined, so that the network does not have a characteristic scale or "size".Preferential attachment and the fitness model have been proposed as mechanisms to explain conjectured power law degree distributions in real networks.In a later paper in 1976, Price also proposed a mechanism to explain the occurrence of power laws in citation networks, which he called "cumulative advantage" but which is today more commonly known under the name preferential attachment.Recent interest in scale-free networks started in 1999 with work by Albert-László Barabási and Réka Albert at the University of Notre Dame who mapped the topology of a portion of the World Wide Web,[5] finding that some nodes, which they called "hubs", had many more connections than others and that the network as a whole had a power-law distribution of the number of links connecting to a node.[8] When the concept of "scale-free" was initially introduced in the context of networks,[5] it primarily referred to a specific trait: a power-law distribution for a given variableThe power-law degree distribution enables us to make "scale-free" assertions about the prevalence of high-degree nodes.[12] The most notable characteristic in a scale-free network is the relative commonness of vertices with a degree that greatly exceeds the average.The highest-degree nodes are often called "hubs", and are thought to serve specific purposes in their networks, although this depends greatly on the domain.Another important characteristic of scale-free networks is the clustering coefficient distribution, which decreases as the node degree increases.Similarly, the clustering coefficient of scale-free networks can vary significantly depending on other topological details.[13] Although many real-world networks are thought to be scale-free, the evidence often remains inconclusive, primarily due to the developing awareness of more rigorous data analysis techniques.A few examples of networks claimed to be scale-free include: Scale free topology has been also found in high temperature superconductors.[18] The qualities of a high-temperature superconductor — a compound in which electrons obey the laws of quantum physics, and flow in perfect synchrony, without friction — appear linked to the fractal arrangements of seemingly random oxygen atoms and lattice distortion.[19] A space-filling cellular structure, weighted planar stochastic lattice (WPSL) has recently been proposed whose coordination number distribution follow a power-law.Erdős and Rényi (1960) studied a model of growth for graphs in which, at each step, two nodes are chosen uniformly at random and a link is inserted between them.They examined communities with interests in a specific topic such as the home pages of universities, public companies, newspapers or scientists, and discarded the major hubs of the Web.Based on these observations, the authors proposed a generative model that mixes preferential attachment with a baseline probability of gaining a link.There are two major components that explain the emergence of the power-law distribution in the Barabási–Albert model: the growth and the preferential attachment.Disassortativity would be found in technological (Internet, World Wide Web) and biological (protein interaction, metabolism) networks.The recipe of Barabási and Albert[26] has been followed by several variations and generalizations[27][28][29][30][22] and the revamping of previous mathematical works.It should also be kept in mind that the fact that "preferential attachment" models give rise to scale-free networks does not prove that this is the mechanism underlying the evolution of real-world scale-free networks, as there might exist different mechanisms at work in real-world systems that nevertheless give rise to scaling.This results in the relative attractiveness of nodes with different degrees changing over time, a feature also observed in real networks.It implies that the higher the links (degree) a node has, the higher its chance of gaining more links since they can be reached in a larger number of ways through mediators which essentially embodies the intuitive idea of rich get richer mechanism (or the preferential attachment rule of the Barabasi–Albert model).is not linear, and recent studies have demonstrated that the degree distribution depends strongly on the shape of the functionKrapivsky, Redner, and Leyvraz[29] demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment.In this case the rate equation leads to This way the exponent of the degree distribution can be tuned to any value between 2 and[clarification needed] Hierarchical network models are, by design, scale free and have high clustering of nodes.This heterogeneous degree distribution then simply reflects the negative curvature and metric properties of the underlying hyperbolic geometry.[37][38] In models of scale-free ideal networks it is possible to demonstrate that Dunbar's number is the cause of the phenomenon known as the 'six degrees of separation'.of a scale-free network is typically done by using the maximum likelihood estimation with the degrees of a few uniformly sampled nodes.