Function composition
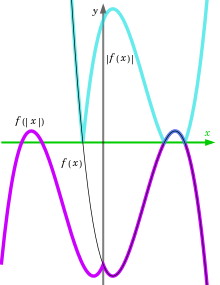
[1] That is, if f, g, and h are composable, then f ∘ (g ∘ h) = (f ∘ g) ∘ h.[2] Since the parentheses do not change the result, they are generally omitted.The inverse function of a composition (assumed invertible) has the property that (f ∘ g)−1 = g−1∘ f−1.[3] Derivatives of compositions involving differentiable functions can be found using the chain rule.Higher derivatives of such functions are given by Faà di Bruno's formula.[4] Suppose one has two (or more) functions f: X → X, g: X → X having the same domain and codomain; these are often called transformations.In general, transformation monoids can have remarkably complicated structure.That is: More generally, for any natural number n ≥ 2, the nth functional power can be defined inductively by f n = f ∘ f n−1 = f n−1 ∘ f, a notation introduced by Hans Heinrich Bürmann[citation needed][10][11] and John Frederick William Herschel.Note: If f takes its values in a ring (in particular for real or complex-valued f ), there is a risk of confusion, as f n could also stand for the n-fold product of f, e.g. f 2(x) = f(x) · f(x).However, for negative exponents (especially −1), it nevertheless usually refers to the inverse function, e.g., tan−1 = arctan ≠ 1/tan.More generally, when gn = f has a unique solution for some natural number n > 0, then f m/n can be defined as gm.Under additional restrictions, this idea can be generalized so that the iteration count becomes a continuous parameter; in this case, such a system is called a flow, specified through solutions of Schröder's equation.Iterated functions and flows occur naturally in the study of fractals and dynamical systems.For the same purpose, f[n](x) was used by Benjamin Peirce[14][11] whereas Alfred Pringsheim and Jules Molk suggested nf(x) instead.[15][11][nb 2] Many mathematicians, particularly in group theory, omit the composition symbol, writing gf for g ∘ f.[16] During the mid-20th century, some mathematicians adopted postfix notation, writing xf for f(x) and (xf)g for g(f(x)).[17] This can be more natural than prefix notation in many cases, such as in linear algebra when x is a row vector and f and g denote matrices and the composition is by matrix multiplication.The order is important because function composition is not necessarily commutative.Having successive transformations applying and composing to the right agrees with the left-to-right reading sequence.Computer scientists may write "f ; g" for this,[18] thereby disambiguating the order of composition.[19] Since all functions are binary relations, it is correct to use the [fat] semicolon for function composition as well (see the article on composition of relations for further details on this notation).Function composition appears in one form or another in numerous programming languages.When g is a simple constant b, composition degenerates into a (partial) valuation, whose result is also known as restriction or co-factor.[21] The partial composition in only one argument mentioned previously can be instantiated from this more general scheme by setting all argument functions except one to be suitably chosen projection functions.[21] The notion of commutation also finds an interesting generalization in the multivariate case; a function f of arity n is said to commute with a function g of arity m if f is a homomorphism preserving g, and vice versa, that is:[21]A binary (or higher arity) operation that commutes with itself is called medial or entropic.A small circle R∘S has been used for the infix notation of composition of relations, as well as functions.The axioms of a category are in fact inspired from the properties (and also the definition) of function composition.[24] The structures given by composition are axiomatized and generalized in category theory with the concept of morphism as the category-theoretical replacement of functions.These structures form dagger categories.The standard "foundation" for mathematics starts with sets and their elements.the membership relation for sets can often be replaced by the composition operation for functions.- Saunders Mac Lane, Mathematics: Form and Function[25]The composition symbol ∘ is encoded as U+2218 ∘ RING OPERATOR (∘, ∘); see the Degree symbol article for similar-appearing Unicode characters.

Function composition (computer science)operator ringoperator assistanceFunctionHistory of the function conceptdomaincodomainX → 𝔹
𝔹
→ X
𝔹n
→ X
X
→ ℤ
ℤ
→ X
X
→ ℝ
ℝ
→ X
ℝn
→ X
X
→ ℂ
ℂ
→ X
ℂn
→ XClasses/propertiesConstantIdentityLinearPolynomialRationalAlgebraicAnalyticSmoothContinuousMeasurableInjectiveSurjectiveBijectiveRestrictionInverseRelationBinary relationSet-valuedMultivaluedPartialImplicitHigher-orderMorphismFunctorList of specific functionsmathematicsfunctionsappliedcomposition of relationsinfinite setreal numberspermutationsassociativesubsetintervalabsolute valuecubic functioncommuteone-to-onebijectionsinverse functionDerivativeschain ruleHigher derivativesFaà di Bruno's formulamultiplicationpointwisecommutativeTransformation monoidtransformationsalgebraic structuremonoidde Rham curvefull transformation semigroupshear mappingtransformation groupgeneratedCayley's theoremisomorphismsymmetric groupregular semigroupIterated functionnatural numberHans Heinrich BürmannJohn Frederick William Herschelfunction iterationnegatedtrigonometryexponentiationtrigonometric functionsfunctional square rootiteration countSchröder's equationfractalsdynamical systemsBenjamin PeirceAlfred PringsheimJules Molkgroup theorypostfix notationprefix notationlinear algebrarow vectormatricesmatrix multiplicationZ notationrelation compositionComposition operatoroperatoroperator theoryprogramming languagesmultivariate functionsprimitive recursive functionprojection functionsoperationsaritieshomomorphismmedial or entropicCompositionbinary relationspartial functionsWagner–Preston theoremcategory of setsmorphismscategorycategory theoryconverse relations