Associative property
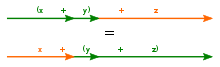
Within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not changed.Even though the parentheses were rearranged on each line, the values of the expressions were not altered.Since this holds true when performing addition and multiplication on any real numbers, it can be said that "addition and multiplication of real numbers are associative operations".Associativity is not the same as commutativity, which addresses whether the order of two operands affects the result.For example, the order does not matter in the multiplication of real numbers, that is, a × b = b × a, so we say that the multiplication of real numbers is a commutative operation.However, operations such as function composition and matrix multiplication are associative, but not (generally) commutative.Associative operations are abundant in mathematics; in fact, many algebraic structures (such as semigroups and categories) explicitly require their binary operations to be associative.However, many important and interesting operations are non-associative; some examples include subtraction, exponentiation, and the vector cross product.In contrast to the theoretical properties of real numbers, the addition of floating point numbers in computer science is not associative, and the choice of how to associate an expression can have a significant effect on rounding error.The associative law can also be expressed in functional notation thus:If a binary operation is associative, repeated application of the operation produces the same result regardless of how valid pairs of parentheses are inserted in the expression.For instance, a product of 3 operations on 4 elements may be written (ignoring permutations of the arguments), inSo unless the expression with omitted parentheses already has a different meaning (see below), the parentheses can be considered unnecessary and "the" product can be written unambiguously as As the number of elements increases, the number of possible ways to insert parentheses grows quickly, but they remain unnecessary for disambiguation." is a metalogical symbol representing "can be replaced in a proof with".The following logical equivalences demonstrate that associativity is a property of particular connectives.[citation needed] Joint denial is an example of a truth functional connective that is not associative.on a set S that does not satisfy the associative law is called non-associative.In Lie algebras, the multiplication satisfies Jacobi identity instead of the associative law; this allows abstracting the algebraic nature of infinitesimal transformations.In mathematics, addition and multiplication of real numbers are associative.By contrast, in computer science, addition and multiplication of floating point numbers are not associative, as different rounding errors may be introduced when dissimilar-sized values are joined in a different order.[7] To illustrate this, consider a floating point representation with a 4-bit significand: Even though most computers compute with 24 or 53 bits of significand,[8] this is still an important source of rounding error, and approaches such as the Kahan summation algorithm are ways to minimise the errors.However, mathematicians agree on a particular order of evaluation for several common non-associative operations.This is simply a notational convention to avoid parentheses.while a right-associative operation is conventionally evaluated from right to left:Left-associative operations include the following: This notation can be motivated by the currying isomorphism, which enables partial application.Repeated powers would mostly be rewritten with multiplication:Formatted correctly, the superscript inherently behaves as a set of parentheses; e.g. in the expressionthe addition is performed before the exponentiation despite there being no explicit parenthesesIn such a case, right-associativity is usually implied.Using right-associative notation for these operations can be motivated by the Curry–Howard correspondence and by the currying isomorphism.Non-associative operations for which no conventional evaluation order is defined include the following.)William Rowan Hamilton seems to have coined the term "associative property"[17] around 1844, a time when he was contemplating the non-associative algebra of the octonions he had learned about from John T.

operator associativityAssociativity (linguistics)rule of replacementElementary algebraBoolean algebraSet theoryLinear algebraPropositional calculusmathematicsbinary operationsparenthesespropositional logicexpressionslogical proofsoperationsoperandsreal numberscommutativityfunction compositionmatrix multiplicationalgebraic structuressemigroupscategoriessubtractionexponentiationvector cross productfloating pointthis diagram commutescomposebinary operationmultiplicationTamari latticeCatalan numberlogical biconditionalconcatenationarithmeticadditioncomplex numbersquaternionsoctonionsgreatest common divisorleast common multipleintersectioncategory theorymatriceslinear functionstotally ordered setTransformation rulesRules of inferenceImplication introductionelimination (modus ponens)Biconditional introductioneliminationConjunction introductionDisjunction introductionDisjunctivehypothetical syllogismConstructivedestructive dilemmaAbsorptionmodus tollensmodus ponendo tollensNegation introductionRules of replacementDouble negationDe Morgan's lawsTranspositionMaterial implicationExportationTautologyPredicate logicUniversal generalizationinstantiationExistential generalizationlogical expressionsmetalogicalsymbollogical connectiveslogical equivalencestautologiesJoint denialDivisionseriesnon-associative algebrasscalar multiplicationLie algebrasJacobi identityinfinitesimal transformationsquasigroupquasifieldnon-associative ringcommutative non-associative magmassignificandKahan summation algorithmorder of evaluationmathematicianscurryingbeforeFunction definitionCurry–Howard correspondenceKnuth's up-arrow operatorscross productaveragerelative complementmaterial nonimplicationWilliam Rowan HamiltonJohn T. GravesLight's associativity testTelescoping seriessemigroupdistributivityPower associativityalternativityflexibilityN-ary associativityMoufang identitiesSpringerThe Art of Computer ProgrammingACM Computing SurveysKhan AcademyWayback MachineHamilton, W.R.Philosophical MagazineTrinity College DublinBaez, John C.