Phonon
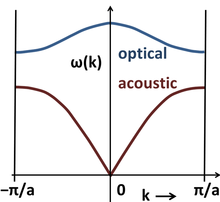
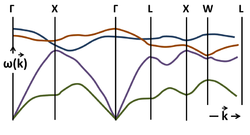
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids.A type of quasiparticle in physics,[1] a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles.A phonon is the quantum mechanical description of an elementary vibrational motion in which a lattice of atoms or molecules uniformly oscillates at a single frequency.Although the electric forces in real solids extend to infinity, this approximation is still valid because the fields produced by distant atoms are effectively screened.It is customary to deal with waves in Fourier space which uses normal modes of the wavevector as variables instead of coordinates of particles.By analogy to the photon case when the electromagnetic field is quantized, the quantum of vibrational energy is called a phonon.In the one-dimensional model, the atoms were restricted to moving along the line, so the phonons corresponded to longitudinal waves.This gives rise to the additional normal coordinates, which, as the form of the Hamiltonian indicates, we may view as independent species of phonons.At low values of k (i.e. long wavelengths), the dispersion relation is almost linear, and the speed of sound is approximately ωa, independent of the phonon frequency.As a result, packets of phonons with different (but long) wavelengths can propagate for large distances across the lattice without breaking apart.For a crystal that has at least two atoms in its primitive cell, the dispersion relations exhibit two types of phonons, namely, optical and acoustic modes corresponding to the upper blue and lower red curve in the diagram, respectively.The lower figure shows the dispersion relations for several phonon modes in GaAs as a function of wavevector k in the principal directions of its Brillouin zone.In general, if there are p atoms (denoted by N earlier) in the primitive unit cell, there will be 3p branches of phonon dispersion in a 3-dimensional crystal.For general anisotropic crystals, the phonon waves are longitudinal or transverse only in certain special symmetry directions.[2] The second quantization technique, similar to the ladder operator method used for quantum harmonic oscillators, is a means of extracting energy eigenvalues without directly solving the differential equations.defined in the quantum treatment section above, we can define creation and annihilation operators:[12] The following commutators can be easily obtained by substituting in the canonical commutation relation: Using this, the operators bk† and bk can be inverted to redefine the conjugate position and momentum as: Directly substituting these definitions for[12] As with the quantum harmonic oscillator, one can show that bk† and bk respectively create and destroy a single field excitation, a phonon, with an energy of ħωk.First, phonons are bosons, since any number of identical excitations can be created by repeated application of the creation operator bk†.If the displacement is in the direction of propagation, then in some areas the atoms will be closer, in others farther apart, as in a sound wave in air (hence the name acoustic).If the wavelength of acoustic phonons goes to infinity, this corresponds to a simple displacement of the whole crystal, and this costs zero deformation energy.They are called optical because in ionic crystals, such as sodium chloride, fluctuations in displacement create an electrical polarization that couples to the electromagnetic field.Optical phonons have a non-zero frequency at the Brillouin zone center and show no dispersion near that long wavelength limit.This is because they correspond to a mode of vibration where positive and negative ions at adjacent lattice sites swing against each other, creating a time-varying electrical dipole moment.In other words, the wave-number in cm−1 units corresponds to the inverse of the wavelength of a photon in vacuum that has the same frequency as the measured phonon.This similarity is not coincidental, for it turns out that the electromagnetic field behaves like a set of harmonic oscillators, giving rise to black-body radiation.Because the difference in energy is what we measure and not the absolute value of it, the constant term 1/2ħωq can be ignored without changing the equations of motion.[20] Recent research has shown that phonons and rotons may have a non-negligible mass and be affected by gravity just as standard particles are.From this, it is predicted that phonons would deflect away as it detects the difference in densities, exhibiting the qualities of a negative gravitational field.Superconductivity is a state of electronic matter in which electrical resistance vanishes and magnetic fields are expelled from the material.[25] They have been also shown to form “phonon winds” where an electric current in a graphene surface is generated by a liquid flow above it due to the viscous forces at the liquid–solid interface.



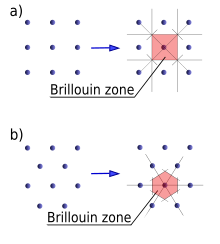
photonPhonon (software)Phonon (company)collective excitationelasticmoleculescondensed mattersolidsliquidsquasiparticlephysicsexcited statequantum mechanicalquantizationmodes of vibrationssound wavesphotonslight wavesthermal conductivityelectrical conductivityneutron scatteringSovietIgor TammYakov Frenkelwave-particle dualityunit cellvibrationallatticefrequencyclassical mechanicsnormal modesuperpositionFourier analysiswave-likeparticle-likewave–particle dualityaxiomscorrespondencecrystallineamorphousAvogadro numberforcesVan der Waals forcescovalent bondselectrostatic attractionselectricMagneticgravitationalpotential energypositionmany-body problemapproximationsscreenedharmonic potentialsTaylor expandingcrystal structurenatural frequencymultiscale Green's functions.amplitudewavelengthNyquist–Shannon sampling theoremnormal modesfrequenciesadiabatic theoremdiscrete Fourier transformharmonic oscillatorsdispersion relationangular frequencywavenumbercontinuum limitscalar field theoryHamiltonianmomentumFourier spacewavevectorperiodicitydiscrete Fourier transformsHermitianzero-point energyquantum harmonic oscillatorenergyelectromagnetic fieldsecond quantizationpolarizationlongitudinal wavestransverse wavesspeed of soundgroup velocityBrillouin zoneprimitive celllongitudinal acoustic modetransverse acoustic modesinelastic neutron scatteringfluidsshear stressesviscoelasticoperatorquantum field theorybosonsladder operatoreigenvaluescreation and annihilation operatorscanonical commutation relationspectrumposition and momentum spacecorrelation functionsodium chlorideinfrared radiationelectrical dipole momentRaman scatteringLyddane–Sachs–Teller relationspeed of light in vacuumCrystal momentummatter wavesreciprocal lattice vectorsBloch electronsthermodynamicdensity of statesheat capacityabsolute zeroground statetemperaturerandomlymean valuephoton gaselectromagnetic cavity