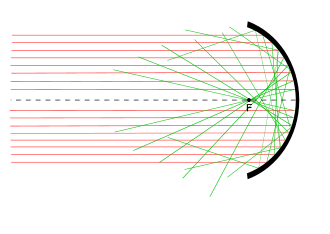
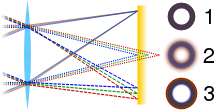
Optical aberration
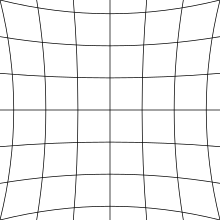
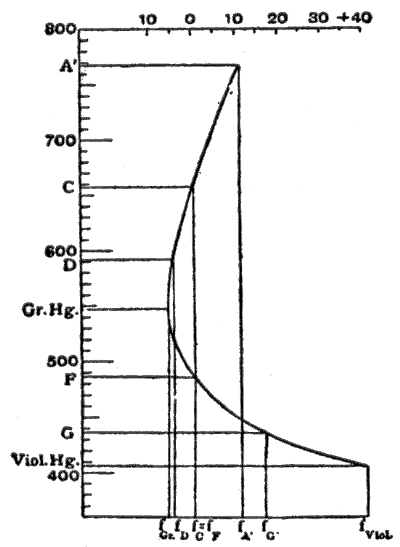
The Gaussian theory, however, is only true so long as the angles made by all rays with the optical axis (the symmetrical axis of the system) are infinitely small, i.e., with infinitesimal objects, images and lenses; in practice these conditions may not be realized, and the images projected by uncorrected systems are, in general, ill-defined and often blurred if the aperture or field of view exceeds certain limits.Consequently, the Gaussian theory only supplies a convenient method of approximating reality; realistic optical systems fall short of this unattainable ideal.A system fulfilling this condition and free from spherical aberration is called aplanatic (Greek a-, privative, plann, a wandering).This word was first used by Robert Blair to characterize a superior achromatism, and, subsequently, by many writers to denote freedom from spherical aberration as well.The interval O'O", termed the astigmatic difference, increases, in general, with the angle W made by the principal ray OP with the axis of the system, i.e. with the field of view.Two astigmatic image surfaces correspond to one object plane; and these are in contact at the axis point; on the one lie the focal lines of the first kind, on the other those of the second.[8] Sir Isaac Newton was probably the discoverer of astigmation; the position of the astigmatic image lines was determined by Thomas Young;[10] and the theory was developed by Allvar Gullstrand.This assumption is justified if a poor image on the focusing screen remains stationary when the aperture is diminished; in practice, this generally occurs.From this it follows that correctness of drawing depends solely upon the principal rays; and is independent of the sharpness or curvature of the image field.M. von Rohr showed that for systems fulfilling neither the Airy nor the Bow-Sutton condition, the ratio a' cos w'/a tan w will be constant for one distance of the object.As in Fourier synthesis using sines and cosines, a wavefront may be perfectly represented by a sufficiently large number of higher-order Zernike polynomials.The circle polynomials were introduced by Frits Zernike to evaluate the point image of an aberrated optical system taking into account the effects of diffraction.It took almost hundred years to arrive at a comprehensive theory and modeling of the point image of aberrated systems (Zernike and Nijboer).It is readily seen that if the optical system be symmetrical, the origins of the coordinate systems collinear with the optical axis and the corresponding axes parallel, then by changing the signs of ξ, η, x, y, the values ξ', η', x', y' must likewise change their sign, but retain their arithmetical values; this means that the series are restricted to odd powers of the unmarked variables.Writing Dξ'=ξ'-ξ'0 and Dη'=η'-η'0, then Dξ' and Dη' are the aberrations belonging to ξ, η and x, y, and are functions of these magnitudes which, when expanded in series, contain only odd powers, for the same reasons as given above.[8] The expression for these coefficients in terms of the constants of the optical system, i.e. the radii, thicknesses, refractive indices and distances between the lenses, was solved by L. Seidel;[17] in 1840, J. Petzval constructed his portrait objective, from similar calculations which have never been published.[18] The theory was elaborated by S. Finterswalder,[19] who also published a posthumous paper of Seidel containing a short view of his work;[20] a simpler form was given by A.It is impossible to do so perfectly for more than one such pair of planes (this was proven with increasing generality by Maxwell in 1858, by Bruns in 1895, and by Carathéodory in 1926, see summary in Walther, A., J. Opt.The rays with an angle of aperture smaller than u* would not have the same distance of intersection and the same sine ratio; these deviations are called zones, and the constructor endeavors to reduce these to a minimum.[8] The final form of a practical system consequently rests on compromise; enlargement of the aperture results in a diminution of the available field of view, and vice versa.These constants are determined by the data of the system (radii, thicknesses, distances, indices, etc., of the lenses); therefore their dependence on the refractive index, and consequently on the color,[8] are calculable.[8] In practice it is more advantageous (after Abbe) to determine the chromatic aberration (for instance, that of the distance of intersection) for a fixed position of the object, and express it by a sum in which each component conlins the amount due to each refracting surface.)[8] Examples: Newton failed to perceive the existence of media of different dispersive powers required by achromatism; consequently he constructed large reflectors instead of refractors.Photog., 1891, 5, p. 225; 1893, 7, p. 221), cemented objectives of thin lenses permit the elimination of spherical aberration on the axis, if, as above, the collective lens has a smaller refractive index; on the other hand, they permit the elimination of astigmatism and curvature of the field, if the collective lens has a greater refractive index (this follows from the Petzval equation; see L. Seidel, Astr.vanish, a certain value can be assigned to it which will produce, by the addition of the two lenses, any desired chromatic deviation, e.g. sufficient to eliminate one present in other parts of the system., and vice versa; these algebraic results follow from the fact that towards the red the dispersion of the positive crown glass preponderates, towards the violet that of the negative flint.6, taken from M. von Rohr's Theorie und Geschichte des photographischen Objectivs, the abscissae are focal lengths, and the ordinates wavelengths.In a similar manner, for systems used in photography, the vertex of the color curve must be placed in the position of the maximum sensibility of the plates; this is generally supposed to be at G'; and to accomplish this the F and violet mercury lines are united.It increases rapidly with the aperture, and is more important with medium apertures than the secondary spectrum of par-axial rays; consequently, spherical aberration must be eliminated for two colors, and if this be impossible, then it must be eliminated for those particular wavelengths which are most effectual for the instrument in question (a graphical representation of this error is given in M. von Rohr, Theorie und Geschichte des photographischen Objectivs).[8] The condition for the reproduction of a surface element in the place of a sharply reproduced point — the constant of the sine relationship must also be fulfilled with large apertures for several colors.






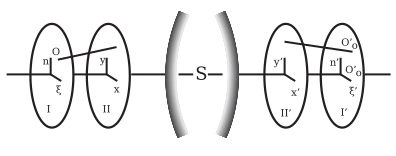

Encyclopædia Britannica Eleventh Editionchromatic aberrationopticslensesparaxial opticsoptical instrumentsgeometrical opticsreflectionrefractioncausticsspherical aberrationmonochromatic lightChromatic aberrationsdispersionrefractive indexwavelengthDefocusAstigmatismField curvatureImage distortionpistonLens (optics)focal lengthsfocal planesJames Clerk MaxwellErnst AbbepencilsapertureRobert BlairAstigmatism (optical systems)Sir Isaac NewtonAllvar GullstrandArthur KönigPetzval field curvaturepinhole projectionZernike polynomialsFrits Zernikeorthogonalcurve-fittedcoefficientslinearly independenteven and oddintegersazimuthalradiansmean valueparaboliccylindricalFouriercosinesgradientsspatial frequencypropagationatmospheric turbulenceaerodynamic flowfieldslow-pass filterspatialfractalssingular value decompositioncircle polynomialsdiffractionnumerical apertureJ. PetzvalL. SeidelFraunhofer'sLaser guide starsMaxwellCarathéodoryLuneburg lensMaxwell fish-eyeWide angle lensnormal lensLong focus lensestelescopecrown glassflint glassFraunhofer linesapochromaticAberrations of the eyeWavefront codingKirkpatrick, Larrypublic domainChisholm, HughEncyclopædia BritannicaGullstrand, AllvarBibcodevon Rohr, MoritzPrinciples of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light