Fixed-point iteration
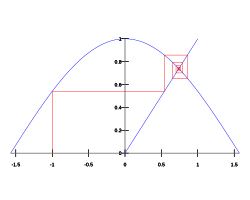
In numerical analysis, fixed-point iteration is a method of computing fixed points of a function.An attracting fixed point of a function f is a fixed point xfix of f with a neighborhood U of "close enough" points around xfix such that for any value of x in U, the fixed-point iteration sequenceThe basin of attraction of xfix is the largest such neighborhood U.[1] The natural cosine function ("natural" means in radians, not degrees or other units) has exactly one fixed point, and that fixed point is attracting.In this case, "close enough" is not a stringent criterion at all—to demonstrate this, start with any real number and repeatedly press the cos key on a calculator (checking first that the calculator is in "radians" mode).It eventually converges to the Dottie number (about 0.739085133), which is a fixed point.That is where the graph of the cosine function intersects the lineAn attracting fixed point is said to be a stable fixed point if it is also Lyapunov stable.A fixed point is said to be a neutrally stable fixed point if it is Lyapunov stable but not attracting.The center of a linear homogeneous differential equation of the second order is an example of a neutrally stable fixed point.The Banach fixed-point theorem gives a sufficient condition for the existence of attracting fixed points.defined on a complete metric space has precisely one fixed point, and the fixed-point iteration is attracted towards that fixed point for any initial guessis defined on the real line with real values and is Lipschitz continuous with Lipschitz constant, and (2) the function f is continuously differentiable in an open neighbourhood of a fixed point xfix, andWhen constructing a fixed-point iteration, it is very important to make sure it converges to the fixed point.We can usually use the Banach fixed-point theorem to show that the fixed point is attractive.Attracting fixed points are a special case of a wider mathematical concept of attractors.Fixed-point iterations are a discrete dynamical system on one variable.Bifurcation theory studies dynamical systems and classifies various behaviors such as attracting fixed points, periodic orbits, or strange attractors.In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the n-th approximation is derived from the previous ones.If this iteration converges to a fixed pointThe speed of convergence of the iteration sequence can be increased by using a convergence acceleration method such as Anderson acceleration and Aitken's delta-squared process.The term chaos game refers to a method of generating the fixed point of any iterated function system (IFS).Starting with any point x0, successive iterations are formed as xk+1 = fr(xk), where fr is a member of the given IFS randomly selected for each iteration.Hence the chaos game is a randomized fixed-point iteration.The chaos game allows plotting the general shape of a fractal such as the Sierpinski triangle by repeating the iterative process a large number of times.More mathematically, the iterations converge to the fixed point of the IFS.Whenever x0 belongs to the attractor of the IFS, all iterations xk stay inside the attractor and, with probability 1, form a dense set in the latter.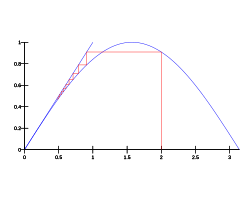

numerical analysisfixed pointsreal numbersdomainsequenceiterated functionconvergemetric spaceBanach fixed-point theoremBabylonian methodsquare rootNewton's methodlinear convergencefixed point iterationfixed pointneighborhoodconvergescosineradiansDottie numberLyapunov stablecontraction mappingcomplete metric spaceLipschitz continuousfixed-point theoremsattractorsdynamical systemBifurcation theoryperiodic orbitsstrange attractorslogistic mapIterative methodroot-finding algorithmquadratic convergenceHalley's methodcubic convergenceRunge–Kutta methodsordinary differential equationA-stabilitycomplex numberPicard–Lindelöf theoremColebrook equationdynamic programmingBellman's functional equationcobweb modelprice theoryconvergence accelerationAnderson accelerationAitken's delta-squared processSteffensen's methodChaos gameiterated function systemfractalSierpinski triangledense setFixed-point combinatorCobweb plotMarkov chainInfinite compositions of analytic functionsRate of convergenceTaylor & FrancisJudd, Kenneth L.Sternberg, ShlomoAntiquitates MathematicaeRoot-finding algorithmsBisection methodRegula falsiITP methodHouseholderQuasi-NewtonBroyden's methodSecant methodNewton–Krylov methodBrent's methodRidders' methodPolynomial methodsAberth methodBairstow's methodDurand–Kerner methodGraeffe's methodJenkins–Traub algorithmLehmer–Schur algorithmLaguerre's methodSplitting circle methodInverse quadratic interpolationMuller's methodSidi's generalized secant method