Contour integration

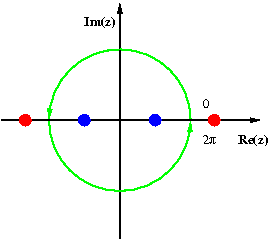
[1][2][3] Contour integration is closely related to the calculus of residues,[4] a method of complex analysis.These requirements correspond to requiring that we consider only curves that can be traced, such as by a pen, in a sequence of even, steady strokes, which stop only to start a new piece of the curve, all without picking up the pen.[6] These provide a precise definition of a "piece" of a smooth curve, of which a contour is made.with a non-vanishing, continuous derivative such that each point is traversed only once (z is one-to-one), with the possible exception of a curve such that the endpoints match (In the case where the endpoints match, the curve is called closed, and the function is required to be one-to-one everywhere else and the derivative must be continuous at the identified point (A directed smooth curve can then be defined as an ordered set of points in the complex plane that is the image of some smooth curve in their natural order (according to the parametrization).Also, a single point in the complex plane is considered a contour.The integral over the curve is the limit of finite sums of function values, taken at the points on the partition, in the limit that the maximum distance between any two successive points on the partition (in the two-dimensional complex plane), also known as the mesh, goes to zero.This means that we use the following method: A fundamental result in complex analysis is that the contour integral of ⁠1/z⁠ is 2πi, where the path of the contour is taken to be the unit circle traversed counterclockwise (or any positively oriented Jordan curve about 0).In the case of the unit circle there is a direct method to evaluate the integralIn evaluating this integral, use the unit circle |z| = 1 as a contour, parametrized by z(t) = eit, with t ∈ [0, 2π], then ⁠dz/dt⁠ = ieit andWe choose a contour that will enclose the real-valued integral, here a semicircle with boundary diameter on the real line (going from, say, −a to a) will be convenient.Call this contour C. There are two ways of proceeding, using the Cauchy integral formula or by the method of residues: Note that:We need to show that the integral over the arc of the semicircle tends to zero as a → ∞, using the estimation lemmaAs an aside, a question can arise whether we do not take the semicircle to include the other singularity, enclosing −i.(which arises in probability theory as a scalar multiple of the characteristic function of the Cauchy distribution) resists the techniques of elementary calculus.Take a to be greater than 1, so that the imaginary unit i is enclosed within the curve.(If t = 0 then the integral yields immediately to real-valued calculus methods and its value is π.)Note that the bounds of integration may as well be π and −π, as in the previous example, or any other pair of endpoints 2π apart.which is in turn computed by summing the residues of f(z)⁠1/iz⁠ inside the unit circle.This affects our choice of the contour C. Normally the logarithm branch cut is defined as the negative real axis, however, this makes the calculation of the integral slightly more complicated, so we define it to be the positive real axis.Then, we use the so-called keyhole contour, which consists of a small circle about the origin of radius ε say, extending to a line segment parallel and close to the positive real axis but not touching it, to an almost full circle, returning to a line segment parallel, close, and below the positive real axis in the negative sense, returning to the small circle in the middle.Now since z1/2 = e(Log z)/2, on the contour outside the branch cut, we have gained 2π in argument along γ.(By Euler's identity, eiπ represents the unit vector, which therefore has π as its log.By using the residue theorem or the Cauchy integral formula (first employing the partial fractions method to derive a sum of two simple contour integrals) one obtainsThis is illustrated in the diagram, where the two black oriented circles are labelled with the corresponding value of the argument of the logarithm used in z3⁄4 and (3 − z)1/4.If we can show that the integrals along the two green circles vanish in the limit, then we also have the value of I, by the Cauchy residue theorem.Integral representations can be important for theoretical reasons, e.g. giving analytic continuation or functional equations, or sometimes for numerical evaluations.For example, the original definition of the Riemann zeta function ζ(s) via a Dirichlet series,where the integration is done over the Hankel contour H, is valid for all complex s not equal to 1.