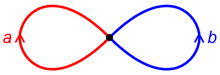
Rose (topology)
Roses are important in algebraic topology, where they are closely related to free groups.As a cell complex, a rose has a single vertex, and one edge for each circle.A rose with n petals can also be obtained by identifying n points on a single circle.The universal cover is an infinite tree, which can be identified with the Cayley graph of the free group.The intermediate covers of the rose correspond to subgroups of the free group.


mathematicstopological spacegluingcirclesalgebraic topologyfree groupsfundamental groupfree groupwedge sumquotient spacecell complextopological graphuniversal covergeneratorCayley graphpresentation complexpresentation of a groupcoverssubgroupsNielsen–Schreier theoremcontractibleEilenberg–MacLane spacecohomologyconnected graphhomotopy equivalentspanning treespheredeformation retractsfundamental polygonHawaiian earringhomeomorphicBouquet graphList of topologiesPetal projectionQuadrifoliumHatcher, AllenMunkres, James R.