Nielsen–Schreier theorem
That is, there exists a set S of elements which generate H, with no nontrivial relations among the elements of S. The Nielsen–Schreier formula, or Schreier index formula, quantifies the result in the case where the subgroup has finite index: if G is a free group of rank n (free on n generators), and H is a subgroup of finite index [G : H] = e, then H is free of rank, and let H be the subgroup consisting of all reduced words of even length (products of an even number of lettersA short proof of the Nielsen–Schreier theorem uses the algebraic topology of fundamental groups and covering spaces.[1] A free group G on a set of generators is the fundamental group of a bouquet of circles, a topological graph X with a single vertex and with a loop-edge for each generator.[7] In any connected topological graph, it is possible to shrink the edges of a spanning tree of the graph, producing a bouquet of circles that has the same fundamental group H. Since H is the fundamental group of a bouquet of circles, it is itself free.[6] The rank of H can be computed using two properties of Euler characteristic that follow immediately from its definition.Now suppose H is a subgroup of the free group G, with index [G:H] = e. The previous part of the proof shows that H is a free group; let r denote the rank of H. Applying the two properties of Euler characteristic for the covering graph Y corresponding to H gives the following:[8] An equivalent proof using homology and the first Betti number of Y is due to Reinhold Baer and Friedrich Levi (1936).The original proof by Schreier forms the Schreier graph in a different way as a quotient of the Cayley graph of G modulo the action of H.[9] According to Schreier's subgroup lemma, a set of generators for a free presentation of H may be constructed from cycles in the covering graph formed by concatenating a spanning tree path from a base point (the coset of the identity) to one of the cosets, a single non-tree edge, and an inverse spanning tree path from the other endpoint of the edge back to the base point.In the proof based on fundamental groups of bouquets, for instance, the axiom of choice appears in the guise of the statement that every connected graph has a spanning tree.The Nielsen–Schreier theorem in turn implies a weaker version of the axiom of choice, for finite sets.His proof involves performing a sequence of Nielsen transformations on the subgroup's generating set that reduce their length (as reduced words in the free group from which they are drawn).[1][13] Otto Schreier proved the Nielsen–Schreier theorem in its full generality in his 1926 habilitation thesis, Die Untergruppen der freien Gruppe, also published in 1927 in Abh.[14][15] The topological proof based on fundamental groups of bouquets of circles is due to Reinhold Baer and Friedrich Levi (1936).Another topological proof, based on the Bass–Serre theory of group actions on trees, was published by Jean-Pierre Serre (1970).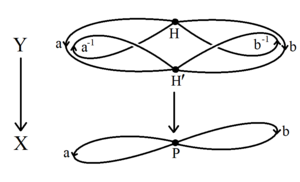
group theorysubgroupfree groupJakob NielsenOtto Schreiergroup presentationset of generatorsreduced wordsstringsconcatenatingisomorphicalgebraic topologyfundamental groupscovering spacesbouquet of circlestopological graphSchreier coset graphspanning treeEuler characteristicbouquethomologyBetti numberReinhold BaerFriedrich LeviCayley graphSchreier's subgroup lemmacyclesaxiom of choiceZermelo–Fraenkel set theorynon-abelianRichard Dedekindfree abelian groupabelianNielsen transformationshabilitationthesisBass–Serre theorygroup actionsJean-Pierre SerreFundamental theorem of cyclic groupscyclic groupsKurosh subgroup theoremRobertson, Edmund F.MacTutor History of Mathematics ArchiveUniversity of St AndrewsBaer, ReinholdLevi, FriedrichFried, Michael D.Jarden, MosheSpringer-VerlagCommentarii Mathematici HelveticiMagnus, WilhelmDover PublicationsNielsen, JakobRotman, Joseph J.Serre, J.-P.Stillwell, John