Bounded variation
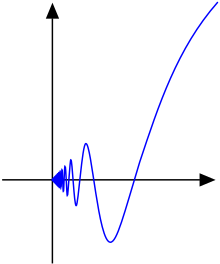
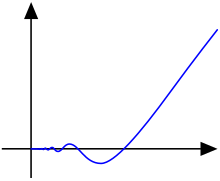
For a continuous function of a single variable, being of bounded variation means that the distance along the direction of the y-axis, neglecting the contribution of motion along x-axis, traveled by a point moving along the graph has a finite value.is said to have bounded variation if its distributional derivative is a vector-valued finite Radon measure.We have the following chains of inclusions for continuous functions over a closed, bounded interval of the real line: According to Boris Golubov, BV functions of a single variable were first introduced by Camille Jordan, in the paper (Jordan 1881) dealing with the convergence of Fourier series.47–48), to extend his direct method for finding solutions to problems in the calculus of variations in more than one variable.Ten years after, in (Cesari 1936), Lamberto Cesari changed the continuity requirement in Tonelli's definition to a less restrictive integrability requirement, obtaining for the first time the class of functions of bounded variation of several variables in its full generality: as Jordan did before him, he applied the concept to resolve of a problem concerning the convergence of Fourier series, but for functions of two variables.After him, several authors applied BV functions to study Fourier series in several variables, geometric measure theory, calculus of variations, and mathematical physics.Olga Arsenievna Oleinik introduced her view of generalized solutions for nonlinear partial differential equations as functions from the space BV in the paper (Oleinik 1957), and was able to construct a generalized solution of bounded variation of a first order partial differential equation in the paper (Oleinik 1959): few years later, Edward D. Conway and Joel A. Smoller applied BV-functions to the study of a single nonlinear hyperbolic partial differential equation of first order in the paper (Conway & Smoller 1966), proving that the solution of the Cauchy problem for such equations is a function of bounded variation, provided the initial value belongs to the same class.Aizik Isaakovich Vol'pert developed extensively a calculus for BV functions: in the paper (Vol'pert 1967) he proved the chain rule for BV functions and in the book (Hudjaev & Vol'pert 1985) he, jointly with his pupil Sergei Ivanovich Hudjaev, explored extensively the properties of BV functions and their application.The total variation of a real-valued (or more generally complex-valued) function f, defined on an intervalIf f is differentiable and its derivative is Riemann-integrable, its total variation is the vertical component of the arc-length of its graph, that is to say, Definition 1.2.on the real line is said to be of bounded variation (BV function) on a chosen intervalThrough the Stieltjes integral, any function of bounded variation on a closed intervalIn this special case,[2] the Riesz–Markov–Kakutani representation theorem states that every bounded linear functional arises uniquely in this way.This point of view has been important in spectral theory,[3] in particular in its application to ordinary differential equations.is said of bounded variation (BV function), and written if there exists a finite vector Radon measureHence the continuous linear functional defines a Radon measure by the Riesz–Markov–Kakutani representation theorem.Precisely, developing this idea for definition 2.2, a local variation is defined as follows, for every setwith respect to the standard topology of finite-dimensional vector spaces, and correspondingly the class of functions of locally bounded variation is defined as There are basically two distinct conventions for the notation of spaces of functions of locally or globally bounded variation, and unfortunately they are quite similar: the first one, which is the one adopted in this entry, is used for example in references Giusti (1984) (partially), Hudjaev & Vol'pert (1985) (partially), Giaquinta, Modica & Souček (1998) and is the following one The second one, which is adopted in references Vol'pert (1967) and Maz'ya (1985) (partially), is the following: Only the properties common to functions of one variable and to functions of several variables will be considered in the following, and proofs will be carried on only for functions of several variables since the proof for the case of one variable is a straightforward adaptation of the several variables case: also, in each section it will be stated if the property is shared also by functions of locally bounded variation or not.In the case of functions of several variables, there are some premises to understand: first of all, there is a continuum of directions along which it is possible to approach a given pointIt is necessary to make precise a suitable concept of limit: choosing a unit vectoris complete respect to it, i.e. it is a Banach space, consider a Cauchy sequenceFinally, again by lower semicontinuity, choosing an arbitrary small positive numberthe following relation holds true: Now, in order to prove that every dense subset ofmust have at least a point inside each member of this family, its cardinality is at least that of the continuum and therefore cannot a be countable subset., defined as A more general chain rule formula for Lipschitz continuous functionsWeighted BV functions were introduced and studied in full generality by Władysław Orlicz and Julian Musielak in the paper Musielak & Orlicz 1959: Laurence Chisholm Young studied earlier the caseSBV functions i.e. Special functions of Bounded Variation were introduced by Luigi Ambrosio and Ennio De Giorgi in the paper (Ambrosio & De Giorgi 1988), dealing with free discontinuity variational problems: given an open subset, since the weak gradient of each function belonging to it consists precisely of the sum of anis bounded: see Halmos (1950, p. 123), Kolmogorov & Fomin (1969, p. 346) or the entry "Total variation" for further details.The book (Hudjaev & Vol'pert 1985) details a very ample set of mathematical physics applications of BV functions.
mathematical analysisfunctiontotal variationgraph of a functioncontinuous functionvariabledistancedirectiony-axisx-axisintersectionhyperplaneRiemann–Stieltjes integralsmonotoneopen subsetdistributional derivativevector-valuedRadon measurealgebradiscontinuous functionsalmost everywheregeneralized solutionsfunctionalsordinarypartial differential equationsmathematicsphysicsengineeringContinuously differentiableLipschitz continuousabsolutely continuousdifferentiableCamille JordanFourier seriesLeonida Tonellidirect methodcalculus of variationsLamberto Cesariintegrabilitygeometric measure theorymathematical physicsRenato CaccioppoliEnnio De GiorgimeasurenonsmoothboundariesCaccioppoli setOlga Arsenievna Oleiniknonlinear partial differential equationsfirst orderJoel A. Smollernonlinear hyperbolic partial differential equationCauchy probleminitial valueAizik Isaakovich Vol'pertLuigi AmbrosioGianni Dal Masocomplexintervalsupremumpartitionsarc-lengthreal lineStieltjes integralbounded linear functionalRiesz–Markov–Kakutani representation theoremprobability measuressemicontinuous functionsspectral theoryordinary differential equationsfunctionsderivative
L
1
(
Ω
)
{\displaystyle L^{1}(\Omega )}
finitevectorlinear functionalvector functionsgradientessential supremumCaccioppoli setscontinuousdifferentiable functionderivativesvariationintegralabsolute valuecontinuous linear functionallinear subspacecontinuouslylinearlyHahn–Banach theoremfunction spacelocally integrable functionsglobally integrable functionsprecompactopen subsetstopologyfinite-dimensionalvector spacesproofslimitscontinuumdirectionsunit vectorsubsetHausdorff measurefunctionallower semi-continuousCauchy sequence
u
∈
L
loc
1
(
Ω
)
{\displaystyle u\in L_{\text{loc}}^{1}(\Omega )}
integrablelower limitlower semicontinuitylinearityvector spacevector subspacecompleteBanach spacecharacteristic functiondense subsetcountablepairwise disjointindexed familyindex setcardinality of the continuumlocal properties
![{\displaystyle [0,2/\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e77efb1ba7f14eb3069f28ca0d9da888ba3c326)