Heat kernel
In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a specified domain with appropriate boundary conditions.It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some auxiliary importance throughout mathematical physics.The heat kernel represents the evolution of temperature in a region whose boundary is held fixed at a particular temperature (typically zero), such that an initial unit of heat energy is placed at a point at time t = 0.The most well-known heat kernel is the heat kernel of d-dimensional Euclidean space Rd, which has the form of a time-varying Gaussian function,[1] This solves the heat equationwhere δ is a Dirac delta distribution and the limit is taken in the sense of distributions, that is, for every function ϕ in the space C∞c(Rd) of smooth functions with compact support, we have[2]On a more general domain Ω in Rd, such an explicit formula is not generally possible.The next simplest cases of a disc or square involve, respectively, Bessel functions and Jacobi theta functions.Nevertheless, the heat kernel still exists and is smooth for t > 0 on arbitrary domains and indeed on any Riemannian manifold with boundary, provided the boundary is sufficiently regular.More precisely, in these more general domains, the heat kernel the solution of the initial boundary value problemIt is not difficult to derive a formal expression for the heat kernel on an arbitrary domain.Consider the Dirichlet problem in a connected domain (or manifold with boundary) U.Let λn be the eigenvalues for the Dirichlet problem of the Laplacian[3]Let ϕn denote the associated eigenfunctions, normalized to be orthonormal in L2(U).The inverse Dirichlet Laplacian Δ−1 is a compact and selfadjoint operator, and so the spectral theorem implies that the eigenvalues of Δ satisfyThe heat kernel has the following expression:Formally differentiating the series under the sign of the summation shows that this should satisfy the heat equation.However, convergence and regularity of the series are quite delicate.The heat kernel is also sometimes identified with the associated integral transform, defined for compactly supported smooth ϕ byThe spectral mapping theorem gives a representation of T in the form the semigroup[4][5]There are several geometric results on heat kernels on manifolds; say, short-time asymptotics, long-time asymptotics, and upper/lower bounds of Gaussian type.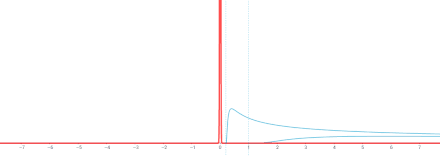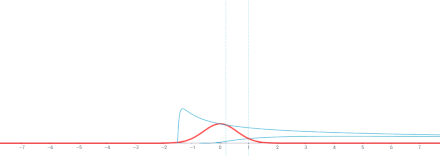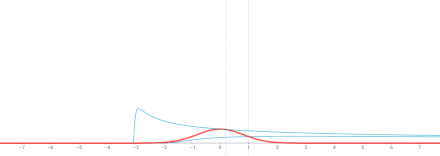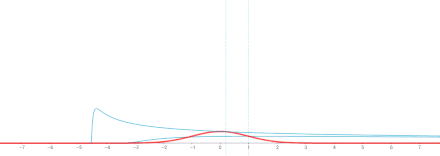
mathematicalheat conductiondiffusionfundamental solutionheat equationboundary conditionsspectrumLaplace operatormathematical physicstemperatureEuclidean spaceGaussian functionDirac delta distributiondistributionsBessel functionsJacobi theta functionssmoothRiemannian manifoldwith boundaryMercer's theoremeigenvaluesLaplacianeigenfunctionscompactselfadjoint operatorspectral theoremintegral transformspectral mapping theoremHeat kernel signatureMinakshisundaram–Pleijel zeta functionMehler kernelSpringer-VerlagAcademic PressEvans, Lawrence C.American Mathematical SocietyFunctional analysistopicsglossaryBanachFréchetHilbertHölderNuclearOrliczSchwartzSobolevTopological vectorBarrelledCompleteLocally convexReflexiveSeparableHahn–BanachRiesz representationClosed graphUniform boundedness principleKrein–MilmanMin–maxGelfand–NaimarkBanach–AlaogluAdjointBoundedHilbert–SchmidtNormalTrace classTransposeUnboundedUnitaryBanach algebraC*-algebraSpectrum of a C*-algebraOperator algebraGroup algebra of a locally compact groupVon Neumann algebraInvariant subspace problemMahler's conjectureHardy spaceSpectral theory of ordinary differential equationsIndex theoremCalculus of variationsFunctional calculusIntegral linear operatorJones polynomialTopological quantum field theoryNoncommutative geometryRiemann hypothesisDistributionGeneralized functionsApproximation propertyBalanced setChoquet theoryWeak topologyBanach–Mazur distanceTomita–Takesaki theory

