Crystal structure
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material.[1] Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter.The smallest group of particles in material that constitutes this repeating pattern is the unit cell of the structure.The collection of symmetry operations of the unit cell is expressed formally as the space group of the crystal structure.That is, the Miller indices are proportional to the inverses of the intercepts of the plane with the unit cell (in the basis of the lattice vectors).However, in these cases the Miller indices are conventionally defined relative to the lattice vectors of the cubic supercell and hence are again simply the Cartesian directions.aP mP mS oP oS oI oF tP tI hR hP cP cI cF The most symmetric, the cubic or isometric system, has the symmetry of a cube, that is, it exhibits four threefold rotational axes oriented at 109.5° (the tetrahedral angle) with respect to each other.In total there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic.By considering the arrangement of atoms relative to each other, their coordination numbers, interatomic distances, types of bonding, etc., it is possible to form a general view of the structures and alternative ways of visualizing them.[9] The principles involved can be understood by considering the most efficient way of packing together equal-sized spheres and stacking close-packed atomic planes in three dimensions.If an additional layer were placed directly over plane A, this would give rise to the following series: This arrangement of atoms in a crystal structure is known as hexagonal close packing (hcp).This is not immediately obvious as the closely packed layers are parallel to the {111} planes of the fcc unit cell.The APFs and CNs of the most common crystal structures are shown below: The 74% packing efficiency of the FCC and HCP is the maximum density possible in unit cells constructed of spheres of only one size.[9] Grain boundaries disrupt the motion of dislocations through a material, so reducing crystallite size is a common way to improve strength, as described by the Hall–Petch relationship.Since grain boundaries are defects in the crystal structure they tend to decrease the electrical and thermal conductivity of the material.The high interfacial energy and relatively weak bonding in most grain boundaries often makes them preferred sites for the onset of corrosion and for the precipitation of new phases from the solid.In nanocrystalline solids, grain boundaries become a significant volume fraction of the material, with profound effects on such properties as diffusion and plasticity.In the limit of small crystallites, as the volume fraction of grain boundaries approaches 100%, the material ceases to have any crystalline character, and thus becomes an amorphous solid.[9] The difficulty of predicting stable crystal structures based on the knowledge of only the chemical composition has long been a stumbling block on the way to fully computational materials design.[17][18] After postulating a direct correlation between electron concentration and crystal structure in beta-phase alloys, Hume-Rothery analyzed the trends in melting points, compressibilities and bond lengths as a function of group number in the periodic table in order to establish a system of valencies of the transition elements in the metallic state.[19] The operation of directional forces were emphasized in one article on the relation between bond hybrids and the metallic structures.The resulting correlation between electronic and crystalline structures is summarized by a single parameter, the weight of the d-electrons per hybridized metallic orbital.The complete morphology of a material is described by polymorphism and other variables such as crystal habit, amorphous fraction or crystallographic defects.This is analogous to ferromagnetism, in that, in the absence of an electric field during production, the ferroelectric crystal does not exhibit a polarization.
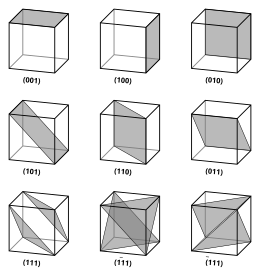

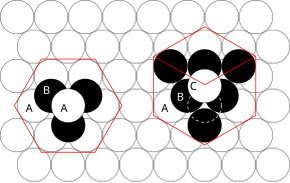
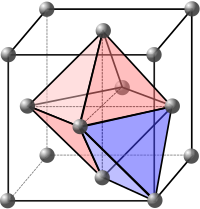

table saltcrystallographymoleculescrystalline materialthree-dimensional spaceunit celltranslationBravais latticelattice constantssymmetryspace groupscleavageelectronic band structureoptical transparencyparallelepipedfractional coordinatesspace groupMiller indexintegersreciprocal latticeplanesOptical propertiesRefractive indexAdsorptionreactivitySurface tensiondefectscrystallitesPlastic deformationDislocationBurgers vectorrotational symmetryCartesian coordinateslattice constantface-centered cubicbody-centered cubicsupercellCartesian directionsprimitive settingCrystal systemtranslational symmetrycrystal systemsSchönflies notationTriclinicMonoclinicOrthorhombicTetragonalHexagonaltetrahedral anglerhombohedraltrigonal crystal systemBravais latticesquasicrystalscrystallographic point groupPoint groupSchönfliesenantiomorphiccentrosymmetriccyclicprismaticKlein fourpyramidaldipyramidalnon-centrosymmetricdihedralalternatingsymmetricImproper rotationClose-packing of equal spheresclose-packedAtomic packing factorCoordination numberGeometryDiamond cubicTetrahedronSimple cubicOctahedronCuboctahedronHexagonal close-packedTriangular orthobicupolaInterstitial siteinterstitial defectsCrystallographic defectelectron spinferromagneticalloyscold workingGrain boundarydislocationssingle crystalHall–Petchelectricalthermal conductivityprecipitationdiffusionplasticityamorphous solidCrystal structure predictionevolutionary algorithmsPauling's rulesLinus Paulingresonating valence bond theoryaxial ratioHume-RotheryQuartzcrystallinesilicaα-quartzβ-quartztridymitecristobalitecoesitestishovitePolymorphismpolymersmineralsmetalsallotropyelemental solidscrystal habitamorphous fractioncrystallographic defectsstablemelting pointsX-ray diffractionsilicon dioxide