Diamond cubic
In crystallography, the diamond cubic crystal structure is a repeating pattern of 8 atoms that certain materials may adopt as they solidify.While the first known example was diamond, other elements in group 14 also adopt this structure, including α-tin, the semiconductors silicon and germanium, and silicon–germanium alloys in any proportion.Many compound semiconductors such as gallium arsenide, β-silicon carbide, and indium antimonide adopt the analogous zincblende structure, where each atom has nearest neighbors of an unlike element.[3] significantly smaller (indicating a less dense structure) than the packing factors for the face-centered and body-centered cubic lattices.[4] Zincblende structures have higher packing factors than 0.34 depending on the relative sizes of their two component atoms.The first-, second-, third-, fourth-, and fifth-nearest-neighbor distances in units of the cubic lattice constant areAlternatively, each point of the diamond cubic structure may be given by four-dimensional integer coordinates whose sum is either zero or one.The total difference in coordinate values between any two points (their four-dimensional Manhattan distance) gives the number of edges in the shortest path between them in the diamond structure.Because the diamond structure forms a distance-preserving subset of the four-dimensional integer lattice, it is a partial cube.Similarly, truss systems that follow the diamond cubic geometry have a high capacity to withstand compression, by minimizing the unbraced length of individual struts.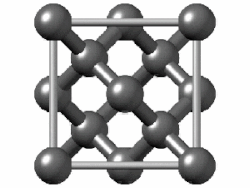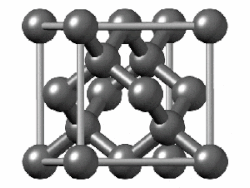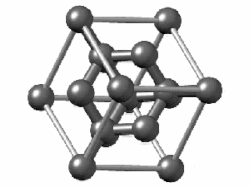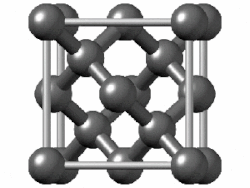




crystal structurePole figurestereographic projection[111] directioncrystallographydiamondgroup 14α-tinsemiconductorssilicongermaniumsilicon–germaniumalloyscristobalitelatticespace groupface-centered cubicBravais latticetetrahedrallybondedprimitive cellcompound semiconductorsgallium arsenidesilicon carbideindium antimonideatomic packing factorface-centered and body-centered cubic latticesinteger latticemoduloManhattan distanceshortest pathdistance-preservingpartial cubetranslational symmetrycongruenceEuclidean spaceLaves graphboron nitridecompressionstrutsstructural rigiditytrianglesoctet trussAllotropes of carbonTriakis truncated tetrahedral honeycombLecture Notes in Computer ScienceBibcodeEppstein, DavidGraph Drawing: 16th International Symposium, GD 2008, Heraklion, Crete, Greece, September 21–24, 2008, Revised PapersSunada, Toshikazu