0.999...
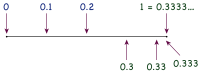
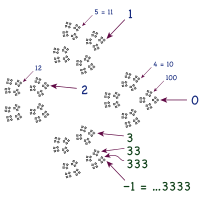
The proofs are generally based on basic properties of real numbers and methods of calculus, such as series and limits.Having values with multiple representations is a feature of all positional numeral systems that represent the real numbers.It is possible to prove the equation 0.999... = 1 using just the mathematical tools of comparison and addition of (finite) decimal numbers, without any reference to more advanced topics such as series and limits.[14] Cheng (2023) concurs, arguing that knowing one can multiply 0.999... by 10 by shifting the decimal point presumes an answer to the deeper question of how one gives a meaning to the expression 0.999... at all.[12] Eisenmann (2008) similarly argues that both the multiplication and subtraction which removes the infinite decimal require further justification.A corresponding proof of the theorem explicitly computes that sequence; it can be found in several proof-based introductions to calculus or analysis.A complementary approach is tailored to the opposite process: for a given real number, define the decimal expansion(s) to name it.[25] The nested intervals theorem is usually founded upon a more fundamental characteristic of the real numbers: the existence of least upper bounds or suprema.Even when a construction is offered, it is usually applied toward proving the axioms of the real numbers, which then support the above proofs.[12] Richman notes that taking Dedekind cuts in any dense subset of the rational numbers yields the same results; in particular, he uses decimal fractions, for which the proof is more immediate.[36] The definition of real numbers as Cauchy sequences was first published separately by Eduard Heine and Georg Cantor, also in 1872.[32] The above approach to decimal expansions, including the proof that 0.999... = 1, closely follows Griffiths & Hilton's 1970 work A comprehensive textbook of classical mathematics: A contemporary interpretation.In other words, the equality 0.999... = 1 holding true is a necessary condition for strings of digits to behave as real numbers should.He calls the proof "an instructive exercise in elementary point-set topology"; it involves viewing sets of positional values as Stone spaces and noticing that their real representations are given by continuous functions.In 1802, H. Goodwyn published an observation on the appearance of 9s in the repeating-decimal representations of fractions whose denominators are certain prime numbers.[47] Investigations in this direction can motivate such concepts as greatest common divisors, modular arithmetic, Fermat primes, order of group elements, and quadratic reciprocity.They must be taken into account to construct a valid proof, applying his 1891 diagonal argument to decimal expansions, of the uncountability of the unit interval.[50] Students of mathematics often reject the equality of 0.999... and 1, for reasons ranging from their disparate appearance to deep misgivings over the limit concept and disagreements over the nature of infinitesimals.Many of these explanations were found by David Tall, who has studied characteristics of teaching and cognition that lead to some of the misunderstandings he has encountered with his college students.[53] Nor are more sophisticated methods foolproof: students who are fully capable of applying rigorous definitions may still fall back on intuitive images when they are surprised by a result in advanced mathematics, including 0.999....The student remained uncomfortable with a limiting argument that 9.99... = 10, calling it a "wildly imagined infinite growing process".[56] With the rise of the Internet, debates about 0.999... have become commonplace on newsgroups and message boards, including many that nominally have little to do with mathematics.[59]A Slate article reports that the concept of 0.999... is "hotly disputed on websites ranging from World of Warcraft message boards to Ayn Rand forums".However, there are mathematically coherent ordered algebraic structures, including various alternatives to the real numbers, which are non-Archimedean.A different definition involves an ultralimit, i.e., the equivalence class [(0.9, 0.99, 0.999, ...)] of this sequence in the ultrapower construction, which is a number that falls short of 1 by an infinitesimal amount.[69] For example, in 1974, Elwyn Berlekamp described a correspondence between strings of red and blue segments in Hackenbush and binary expansions of real numbers, motivated by the idea of data compression.After defining multiplication, the decimal numbers form a positive, totally ordered, commutative semiring.Whether or not that makes sense, the intuitive goal is clear: adding a 1 to the final 9 in 0.999... would carry all the 9s into 0s and leave a 1 in the ones place.A third derivation was invented by a seventh-grader who was doubtful over her teacher's limiting argument that 0.999... = 1 but was inspired to take the multiply-by-10 proof above in the opposite direction: if[73] As a final extension, since 0.999... = 1 (in the reals) and ...999 = −1 (in the 10-adics), then by "blind faith and unabashed juggling of symbols"[75] one may add the two equations and arrive at ...999.999... = 0.



mathematicsrepeating decimalnumberselementary arithmeticpositive real numbernatural numberArchimedean propertyreal numbersintuitivemathematically rigorousproofsfinite decimalscalculusserieslimitsmathematics educationterminating decimalpositional numeral systemsdecimal numbersnumber linenumber systemshyperreal numbersinfinitesimalsinfinite numbersleast upper boundaxiomsreal number systemcompleteness axiomequals signcompletenesscancellableReal analysisDecimal representationinfinite seriesconvergencegeometric seriesLeonhard EulerElements of Algebrabase-4sequenceheuristicsNested intervalsclosed intervalnested intervals theoremintersectionleast upper boundssupremaTom ApostolConstruction of the real numbersstructures built upon the rational numbersaxiomatic set theorynatural numbersintegersrational numbersorderingDedekind cutsCauchy sequencesDedekind cutinfinite setRichard DedekindMathematics Magazinedense subsetdecimal fractionsCauchy sequenceEduard HeineGeorg Cantorsecondary schoolsradix pointfractional partequivalence relationDense orderbinary numeral systemternary numeral systemgolden ratio basealmost allPaul ErdősPaola LoretiKomornik–Loreti constantThue–Morse sequencethe most general positional numeral systemsbalanced ternaryfactorial number systempoint-set topologyStone spacescontinuous functionsnumber theoryprime numbersMidy's theoremgreatest common divisorsmodular arithmeticFermat primesquadratic reciprocityCantor setfractalsunit intervalhis 1891 diagonal argumentuncountabilityparadoxcounterexamplesDavid Tallsupremumlong divisionAPOS TheoryInternetnewsgroupsmessage boardsThe Straight DopeWorld of WarcraftAyn Randmathematical jokesscrew in a lightbulbnumber systemTimothy GowersInfinitesimalalgebraic structuresNon-standard analysisA. H. Lightstonehypernaturaltransfer principlelimit of the sequenceultrapower constructionIan StewartCombinatorial game theoryElwyn BerlekampHackenbushdata compression