Strahler number
These numbers were first developed in hydrology, as a way of measuring the complexity of rivers and streams, by Robert E. Horton (1945) and Arthur Newell Strahler (1952, 1957).The same numbers also arise in the analysis of L-systems and of hierarchical biological structures such as (biological) trees and animal respiratory and circulatory systems, in register allocation for compilation of high-level programming languages and in the analysis of social networks.All trees in this context are directed graphs, oriented from the root towards the leaves; in other words, they are arborescences.A later review of the relationships confirmed this argument, establishing that, from the properties the laws describe, no conclusion can be drawn to explain the structure or origin of the stream network.[7] Gleyzer et al. (2004) describe how to compute Strahler stream order values in a GIS application.The input to their algorithm is a network of the centre lines of the bodies of water, represented as arcs (or edges) joined at nodes.Lake boundaries and river banks should not be used as arcs, as these will generally form a non-tree network with an incorrect topology.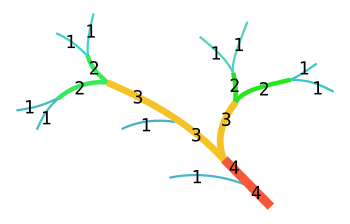

mathematicshydrologyRobert E. HortonArthur Newell StrahlertributariesL-systemsregister allocationcompilationhigh-level programming languagessocial networksdirected graphsarborescencesdegreeAlgorithmicallydepth-first searchpostordercomplete binary treehomeomorphically embeddedbinary treeuniformly at random among all possible binary treesstream orderperennialAmazonOhio RiverMississippi Riverheadwater streamsdrainage basinArcGIS Prostream ordering systemshigh-level programming languageassembly languageregistersSethi–Ullman algorithmpathwidthundirected graphinterval graphcliqueMain stemPfafstetter Coding SystemBibcodeDevroye, LucDevroye, L.Ehrenfeucht, A.Rozenberg, G.Ershov, A. P.Communications of the ACMFlajolet, P.Vuillemin, J.Horton, R. E.Strahler, A. N.River morphologyAlluvial plainDrainage system (geomorphology)EstuaryRiver valleyRiver deltaRiver sinuosityAlluvial riversAnabranchAvulsion (river)Bar (river morphology)Braided riverChannel patternCut bankFloodplainMeanderMeander cutoffMouth barOxbow lakePoint barRiffleRapidsRiparian zoneRiver bifurcationRiver channel migrationRiver mouthSlip-off slopeStream poolThalwegBedrock riverCanyonKnickpointPlunge poolBedformsAntiduneCurrent rippleAggradationBase levelDegradation (geology)Erosion and tectonicsRiver rejuvenationDeposition (geology)Exner equationHack's lawHelicoidal flowPlayfair's lawSediment transportList of rivers that have reversed direction