Stiff equation

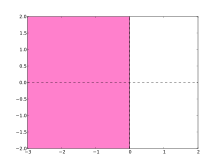
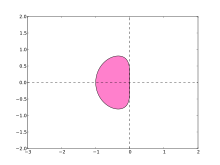
It has proven difficult to formulate a precise definition of stiffness, but the main idea is that the equation includes some terms that can lead to rapid variation in the solution.When integrating a differential equation numerically, one would expect the requisite step size to be relatively small in a region where the solution curve displays much variation and to be relatively large where the solution curve straightens out to approach a line with slope nearly zero.In order for a numerical method to give a reliable solution to the differential system sometimes the step size is required to be at an unacceptably small level in a region where the solution curve is very smooth.One of the most prominent examples of the stiff ordinary differential equations (ODEs) is a system that describes the chemical reaction of Robertson:[1]However, if the interval is very large (1011 say), then many standard codes fail to integrate it correctly.Consider the linear constant coefficient inhomogeneous system where"Phenomenon" is probably a more appropriate word than "property", since the latter rather implies that stiffness can be defined in precise mathematical terms; it turns out not to be possible to do this in a satisfactory manner, even for the restricted class of linear constant coefficient systems.J. D. Lambert defines stiffness as follows: If a numerical method with a finite region of absolute stability, applied to a system with any initial conditions, is forced to use in a certain interval of integration a step length which is excessively small in relation to the smoothness of the exact solution in that interval, then the system is said to be stiff in that interval.Nonetheless, definitions based upon these characteristics are in common use by some authors and are good clues as to the presence of stiffness.Lambert refers to these as "statements" rather than definitions, for the aforementioned reasons.According to Joseph Oakland Hirschfelder, the term "stiff" is used because such systems correspond to tight coupling between the driver and driven in servomechanisms.L. Burden and J. Douglas Faires, Significant difficulties can occur when standard numerical techniques are applied to approximate the solution of a differential equation when the exact solution contains terms of the formProblems involving rapidly decaying transient solutions occur naturally in a wide variety of applications, including the study of spring and damping systems, the analysis of control systems, and problems in chemical kinetics.Both eigenvalues have negative real part and the stiffness ratio is which is fairly large.[6] (while "large" is not a clearly-defined term, but the larger the above quantities are, the more pronounced will be the effect of stiffness.)The exact solution to (10) is Equation 13 behaves quite similarly to a simple exponentialterm, even with a small coefficient, is enough to make the numerical computation very sensitive to step size.Stable integration of (10) requires a very small step size until well into the smooth part of the solution curve, resulting in an error much smaller than required for accuracy.A-stable methods do not exhibit the instability problems as described in the motivating example.which is just inside the stability region and the numerical results converge to zero, albeit rather slowly.Consider the trapezoidal method when applied to the test equationIn fact, the stability region is identical to the left half-plane, and thus the numerical solution ofThis led to the concept of L-stability: a method is L-stable if it is A-stable andExplicit Runge–Kutta methods have a strictly lower triangular coefficient matrixThe stability function of implicit Runge–Kutta methods is often analyzed using order stars.A method is A-stable if and only if its stability function has no poles in the left-hand plane and its order star contains no purely imaginary numbers.[9] Linear multistep methods have the form Applied to the test equation, they become which can be simplified to whereThe region of absolute stability for a multistep method of the above form is then the set of allAgain, if this set contains the left half-plane, the multi-step method is said to be A-stable.The latter result is known as the second Dahlquist barrier; it restricts the usefulness of linear multistep methods for stiff equations.