Morse theory
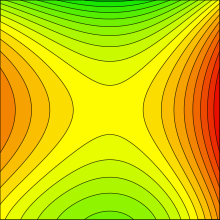
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold.According to the basic insights of Marston Morse, a typical differentiable function on a manifold will reflect the topology quite directly.Morse theory allows one to find CW structures and handle decompositions on manifolds and to obtain substantial information about their homology.Morse originally applied his theory to geodesics (critical points of the energy functional on the space of paths).These techniques were used in Raoul Bott's proof of his periodicity theorem.(more generally, the Jacobian matrix acting as a linear map between tangent spaces does not have maximal rank).does not change except when the water either (1) starts filling a basin, (2) covers a saddle (a mountain pass), or (3) submerges a peak.To these three types of critical points—basins, passes, and peaks (i.e. minima, saddles, and maxima)—one associates a number called the index, the number of independent directions in whichis a disk, which is homotopy equivalent to a point (a 0-cell) which has been "attached" to the empty set.is a cylinder, and is homotopy equivalent to a disk with a 1-cell attached (image at left).is a torus with a disk removed, which is homotopy equivalent to a cylinder with a 1-cell attached (image at right).This does not address what happens when two critical points are at the same height, which can be resolved by a slight perturbation ofIn the case of a landscape or a manifold embedded in Euclidean space, this perturbation might simply be tilting slightly, rotating the coordinate system.One must take care to make the critical points non-degenerate.is called a non-degenerate critical point; if the Hessian is singular thenA less trivial example of a degenerate critical point is the origin of the monkey saddle.This corresponds to the intuitive notion that the index is the number of directions in whichThe degeneracy and index of a critical point are independent of the choice of the local coordinate system used, as shown by Sylvester's Law.As a corollary of the Morse lemma, one sees that non-degenerate critical points are isolated.These results generalize and formalize the 'rule' stated in the previous section.Using the two previous results and the fact that there exists a Morse function on any differentiable manifold, one can prove that any differentiable manifold is a CW complex with anMorse theory can be used to prove some strong results on the homology of manifolds.Using the fact that the alternating sum of the ranks of the homology groups of a topological space is equal to the alternating sum of the ranks of the chain groups from which the homology is computed, then by using the cellular chain groups (see cellular homology) it is clear that the Euler characteristicThis gives a powerful tool to study manifold topology.Suppose on a closed manifold there exists a Morse functionis possible only in a small number of low dimensions, and M is homeomorphic to an Eells–Kuiper manifold.In 1982 Edward Witten developed an analytic approach to the Morse inequalities by considering the de Rham complex for the perturbed operatorIt is defined using a generic choice of Morse function and Riemannian metric.The basic theorem is that the resulting homology is an invariant of the manifold (that is, independent of the function and metric) and isomorphic to the singular homology of the manifold; this implies that the Morse and singular Betti numbers agree and gives an immediate proof of the Morse inequalities.Frederic Bourgeois sketched an approach in the course of his work on a Morse–Bott version of symplectic field theory, but this work was never published due to substantial analytic difficulties.


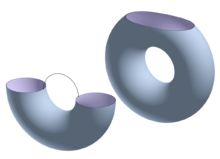
Morse potentialmathematicsdifferential topologytopologymanifolddifferentiable functionsMarston MorseCW structureshandle decompositionshomologyArthur CayleyJames Clerk Maxwelltopographygeodesicscritical pointsenergyfunctionalRaoul Bottperiodicity theoremPicard–Lefschetz theoryfunctioninverse imagecontour linelevel setconnected componentsimple closed curvedouble point(s)saddle pointscritical pointgradientJacobian matrixlinear maptangent spacesmountain passindependentdimensiontangent spaceHessianhomotopy equivalentcylinderembeddedEuclidean spacesmooth functiondifferentiable manifolddifferentialcritical valuesHessian matrixmonkey saddleSylvester's LawneighborhoodisolatedMorse–Palais lemmagenericcompactdiffeomorphicdeformation retractsgradient-like vector fieldscellular homologyEuler characteristicBetti numberGeorges ReebReeb sphere theoremEells–Kuiper manifoldEdward Wittende Rham complexconnected sumreal projective spacesMorse homologysmooth manifoldsRiemannian metricBetti numberssymplectic geometryFloer homologyBott periodicity theoremRound functionsspectral sequenceAlmgren–Pitts min-max theoryDigital Morse theoryDiscrete Morse theoryJacobi setLagrangian GrassmannianLusternik–Schnirelmann categoryMorse–Smale systemMountain pass theoremSard's lemmaStratified Morse theoryJ. Differential Geom.Bott, RaoulPublications Mathématiques de l'IHÉSBulletin of the American Mathematical SocietyThe Philosophical MagazineDover Book on MathematicsLang, SergeGraduate Texts in MathematicsSpringer-VerlagMilnor, JohnManifoldsGlossaryTopological manifoldDifferentiable/Smooth manifoldDifferential structureSmooth atlasSubmanifoldRiemannian manifoldSmooth mapSubmersionPushforwardDifferential formVector fieldAtiyah–Singer indexDarboux'sFrobeniusGeneralized StokesHopf–RinowNoether'sSard'sWhitney embeddingDiffeomorphismGeodesicExponential mapin Lie theoryFoliationImmersionIntegral curveLie derivativeSection


