Exercise (mathematics)
Stephen Leacock described this type:[1] A distinction between an exercise and a mathematical problem was made by Alan H. Schoenfeld:[2] He advocated setting challenges: A similar sentiment was expressed by Marvin Bittinger when he prepared the second edition[3] of his textbook: The zone of proximal development for each student, or cohort of students, sets exercises at a level of difficulty that challenges but does not frustrate them.Some comments in the preface of a calculus textbook[4] show the central place of exercises in the book: This text includes "Functions and Graphs in Applications" (Ch 0.6) which is fourteen pages of preparation for word problems.At the Russian School of Mathematics, students begin multi-step problems as early as the first grade, learning to build on previous results to progress towards the solution.[11] In about 980 Al-Sijzi wrote his Ways of Making Easy the Derivation of Geometrical Figures, which was translated and published by Jan Hogendijk in 1996.Recorde was writing mainly for those who were teaching themselves, scholars who would have no one to check their answers to the exercises.In Europe before 1900, the science of graphical perspective framed geometrical exercises.Felix Klein described preparation for the entrance examination of École Polytechnique as[17] Sylvestre Lacroix was a gifted teacher and expositor.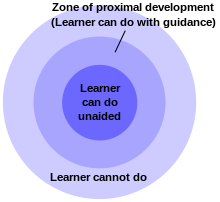
algebramathematicsMathematics teachersadditionsubtractionmultiplicationdivisionintegersschoolarithmeticrational numbersgeometryanglessegmentstrianglestrigonometrytrigonometric identitiesfunctionstheoremscalculusderivativesintegralsSchaum's OutlinesLev Vygotskyelementary algebrafactorizationpolynomialscompleting the squarequadratic polynomialword problemStephen Leacockfractionsmathematical problemAlan H. Schoenfeldzone of proximal developmentfinite fieldstextbookproofsJ. C. Maxwelllanguage of mathematicsproblem solvingproprietaryToru KumonKumon methodRussian School of MathematicsRussianW. H. Freeman and Companycounting rodsrod calculussuanpanBook on Numbers and ComputationNine Chapters on the Mathematical Artlinear algebraAl-SijziJan HogendijkArabic languageNatureRobert RecordeThe Ground of Artstextbooksgraphical perspectiveBrook Taylorwriting slatesFelix Kleinentrance examinationÉcole PolytechniqueSylvestre LacroixMathematical triposCambridge UniversityFranz Ernst Neumannproblem setsStephen TimoshenkoPetersburg State University of Means of CommunicationAlgorithmWorked-example effectThe Mathematical MagpieClifton FadimanSimon & SchusterAddison WesleyPrentice HallCambridge University PressW. D. NivenInternet ArchiveI. M. YaglomD. K. FaddeevJoel Lee BrennerAleksei Fedorovich FilippovJHU PressG. B. MathewsUniversity of Wales PressKirsti AndersenMath Sci PressS. F. LacroixUniversity of Chicago PressD. Van Nostrand CompanyTatyana AfanasyevaPacific Institute for the Mathematical SciencesVladimir ArnoldJames Alfred EwingMathematics educationUnited StatesNew YorkUnited KingdomTraditionalThree-part lessonSingaporeReformComputer-basedModern elementaryInformalCognitively guidedCritical