Cauchy distribution
In mathematics, it is closely related to the Poisson kernel, which is the fundamental solution for the Laplace equation in the upper half-plane.in the x-y plane, and select a line passing through the point, with its direction (angle with theare two independent normally distributed random variables with expected value 0 and variance 1, then the ratiois the scale parameter which specifies the half-width at half-maximum (HWHM), alternativelypositive-semidefinite covariance matrix with strictly positive diagonal entries, then for independent and identically distributedIn addition, the family of Cauchy-distributed random variables is closed under linear fractional transformations with real coefficients.In particular, the average does not converge to the mean, and so the standard Cauchy distribution does not follow the law of large numbers.This can be proved by repeated integration with the PDF, or more conveniently, by using the characteristic function of the standard Cauchy distribution (see below):We see that there is no law of large numbers for any weighted sum of independent Cauchy distributions.This shows that the condition of finite variance in the central limit theorem cannot be dropped.The characteristic function of the Cauchy distribution is given by which is just the Fourier transform of the probability density.The original probability density may be expressed in terms of the characteristic function, essentially by using the inverse Fourier transform: The nth moment of a distribution is the nth derivative of the characteristic function evaluated at[12] Closed-form expression for the total variation, Jensen–Shannon divergence, Hellinger distance, etc.But in the case of the Cauchy distribution, both the terms in this sum (2) are infinite and have opposite sign.[15] When the mean of a probability distribution function (PDF) is undefined, no one can compute a reliable average over the experimental data points, regardless of the sample's size.Various results in probability theory about expected values, such as the strong law of large numbers, fail to hold for the Cauchy distribution.Odd-powered raw moments, however, are undefined, which is distinctly different from existing with the value of infinity.The variance—which is the second central moment—is likewise non-existent (despite the fact that the raw second moment exists with the value infinity).Because the parameters of the Cauchy distribution do not correspond to a mean and variance, attempting to estimate the parameters of the Cauchy distribution by using a sample mean and a sample variance will not succeed.Similarly, calculating the sample variance will result in values that grow larger as more observations are taken.Other, more precise and robust methods have been developed [20][21] For example, the truncated mean of the middle 24% of the sample order statistics produces an estimate for[22][23] However, because of the fat tails of the Cauchy distribution, the efficiency of the estimator decreases if more than 24% of the sample is used.[24] Also, while the maximum likelihood estimator is asymptotically efficient, it is relatively inefficient for small samples.by taking the first derivative produces the following system of equations: Note that is a monotone function in[23][27] The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator ofThe shape can be estimated using the median of absolute values, since for location 0 Cauchy variablesA function with the form of the density function of the Cauchy distribution was studied geometrically by Fermat in 1659, and later was known as the witch of Agnesi, after Maria Gaetana Agnesi included it as an example in her 1748 calculus textbook.[36] Poisson noted that if the mean of observations following such a distribution were taken, the standard deviation did not converge to any finite number.As such, Laplace's use of the central limit theorem with such a distribution was inappropriate, as it assumed a finite mean and variance.Despite this, Poisson did not regard the issue as important, in contrast to Bienaymé, who was to engage Cauchy in a long dispute over the matter.
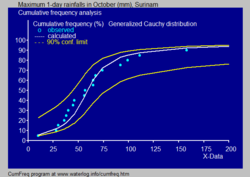

Lorenz curveLorenz systemParameterslocationSupportQuantileundefinedMedianVarianceSkewnessExcess kurtosisEntropyFisher informationAugustin-Louis Cauchycontinuous probability distributionphysicistsHendrik Lorentznormally distributedpathologicalexpected valuemomentsmoment generating functionmathematicsPoisson kernelfundamental solutionLaplace equationupper half-planestable distributionsnormal distributionLévy distributionrandom variablesprobability density functionlocation parameterscale parameterfull width at half maximuminterquartile rangeprobable errorLorentzian functionnascent delta functionDirac delta functioninfinitesimalcumulative distribution functionquantile functionarctangent functionStudent's t-distributionindependent and identically distributedcategorical distributioninfinitely divisible probability distributionstablelocation-scale familylinear transformationslinear fractional transformationsMcCullagh's parametrization of the Cauchy distributionssample meancharacteristic functioncentral limit theoremFourier transformdifferentiableKullback–Leibler divergencef-divergencetotal variationJensen–Shannon divergenceHellinger distancedifferential entropymaximum entropy probability distributionprobability distributiondensity functionimproper integralCauchy principal valueexpected valuesstrong law of large numbersraw momentscentral momentsstandardized momentsHölder's inequalitytruncated distributioni.i.d.circular Cauchy distributiontruncated meanorder statisticsfat tailsMaximum likelihoodnumericalNewton's methodStudent's t distributionPearson distributionstable distributionhyperbolic distributionwrapped Cauchy distributionrandom vectorhomogeneous functionstatistically independentmultivariate Student distributionspectroscopyspectral lineshomogeneous broadeningexponential growthCumFreqdistribution fittinghydrologyconfidence beltbinomial distributionplotting positionscumulative frequency analysiselectrical permittivitycomputational financevalue at riskGaussian DistributionRelativistic Breit–Wigner distributionnuclearparticle physicsresonanceFermatwitch of AgnesiMaria Gaetana AgnesiPoissonstandard deviationLaplaceBienayméLévy flightLévy processLaplace distributionCauchy processStable processSlash distributionThe Annals of Statistics