Linear equation
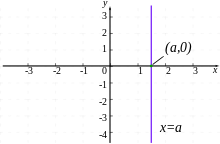
The coefficients may be considered as parameters of the equation and may be arbitrary expressions, provided they do not contain any of the variables.The solutions of such an equation are the values that, when substituted for the unknowns, make the equality true.Often, the term linear equation refers implicitly to this particular case, in which the variable is sensibly called the unknown.In the case of two variables, each solution may be interpreted as the Cartesian coordinates of a point of the Euclidean plane.The solutions of a linear equation form a line in the Euclidean plane, and, conversely, every line can be viewed as the set of all solutions of a linear equation in two variables.This is the origin of the term linear for describing this type of equation.More generally, the solutions of a linear equation in n variables form a hyperplane (a subspace of dimension n − 1) in the Euclidean space of dimension n. Linear equations occur frequently in all mathematics and their applications in physics and engineering, partly because non-linear systems are often well approximated by linear equations.So, for this definition, the above function is linear only when c = 0, that is when the line passes through the origin.Each solution (x, y) of a linear equation may be viewed as the Cartesian coordinates of a point in the Euclidean plane.With this interpretation, all solutions of the equation form a line, provided that a and b are not both zero.Conversely, every line is the set of all solutions of a linear equation.If b ≠ 0, the line is the graph of the function of x that has been defined in the preceding section.In the following subsections, a linear equation of the line is given in each case.A non-vertical line can be defined by its slope m, and its y-intercept y0 (the y coordinate of its intersection with the y-axis).In this case, its linear equation can be written If, moreover, the line is not horizontal, it can be defined by its slope and its x-intercept x0.In this case, its equation can be written or, equivalently, These forms rely on the habit of considering a nonvertical line as the graph of a function.In this case, a linear equation of the line is or This equation can also be written for emphasizing that the slope of a line can be computed from the coordinates of any two points.A line that is not parallel to an axis and does not pass through the origin cuts the axes into two different points.The intercept values x0 and y0 of these two points are nonzero, and an equation of the line is[3] (It is easy to verify that the line defined by this equation has x0 and y0 as intercept values).There are several ways to write a linear equation of this line.Thus, a point-slope form is[3] By clearing denominators, one gets the equation which is valid also when x1 = x2 (for verifying this, it suffices to verify that the two given points satisfy the equation).This form is not symmetric in the two given points, but a symmetric form can be obtained by regrouping the constant terms: (exchanging the two points changes the sign of the left-hand side of the equation).The two-point form of the equation of a line can be expressed simply in terms of a determinant.can be obtained by expanding with respect to its first row the determinant in the equation Besides being very simple and mnemonic, this form has the advantage of being a special case of the more general equation of a hyperplane passing through n points in a space of dimension n – 1.These equations rely on the condition of linear dependence of points in a projective space.A linear equation with more than two variables may always be assumed to have the form The coefficient b, often denoted a0 is called the constant term (sometimes the absolute term in old books[4][5]).Depending on the context, the term coefficient can be reserved for the ai with i > 0.For an equation to be meaningful, the coefficient of at least one variable must be non-zero.The n-tuples that are solutions of a linear equation in n variables are the Cartesian coordinates of the points of an (n − 1)-dimensional hyperplane in an n-dimensional Euclidean space (or affine space if the coefficients are complex numbers or belong to any field).If a linear equation is given with aj ≠ 0, then the equation can be solved for xj, yielding If the coefficients are real numbers, this defines a real-valued function of n real variables.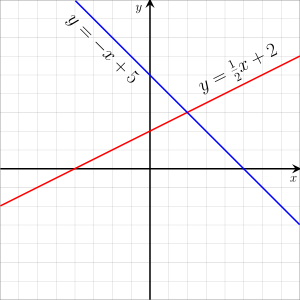

Linear differential equationmathematicsequationvariablesunknownscoefficientsreal numbersparametersexpressionslinear polynomialsolutionsCartesian coordinatesEuclidean planehyperplaneEuclidean spacephysicsengineeringnon-linear systemscomplexsystem of linear equationsLinear function (calculus)functiony-interceptcalculuslinear algebralinear functionaffine functionslinear mapsgraph of the functiongraph of a functionclearing denominatorsdeterminantlinear dependenceprojective spaceaffine spacereal-valuedfunction of n real variablesLinear equation over a ringAlgebraic equationLine coordinatesLinear inequalityNonlinear equationEncyclopedia of MathematicsEMS PressPolynomialspolynomial functionsdegreeZero polynomial (degree undefined or −1 or −∞)Constant function (0)Linear function (1)Quadratic function (2)Quadratic equationCubic function (3)Cubic equationQuartic function (4)Quartic equationQuintic function (5)Sextic equation (6)Septic equation (7)UnivariateBivariateMultivariateMonomialBinomialTrinomialIrreducibleSquare-freeHomogeneousQuasi-homogeneousFactorizationGreatest common divisorDivisionHorner's method of evaluationPolynomial identity testingResultantDiscriminantGröbner basis