Integer partition
Two sums that differ only in the order of their summands are considered the same partition.An individual summand in a partition is called a part.The notation λ ⊢ n means that λ is a partition of n. Partitions can be graphically visualized with Young diagrams or Ferrers diagrams.They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representation theory in general.For example, the partition 2 + 2 + 1 might instead be written as the tuple (2, 2, 1) or in the even more compact form (22, 1) where the superscript indicates the number of repetitions of a part.This multiplicity notation for a partition can be written alternatively asThere are two common diagrammatic methods to represent partitions: as Ferrers diagrams, named after Norman Macleod Ferrers, and as Young diagrams, named after Alfred Young.Both have several possible conventions; here, we use English notation, with diagrams aligned in the upper-left corner.The 14 circles are lined up in 4 rows, each having the size of a part of the partition.Thus, the Young diagram for the partition 5 + 4 + 1 is while the Ferrers diagram for the same partition is While this seemingly trivial variation does not appear worthy of separate mention, Young diagrams turn out to be extremely useful in the study of symmetric functions and group representation theory: filling the boxes of Young diagrams with numbers (or sometimes more complicated objects) obeying various rules leads to a family of objects called Young tableaux, and these tableaux have combinatorial and representation-theoretic significance.[1] As a type of shape made by adjacent squares joined together, Young diagrams are a special kind of polyomino.is No closed-form expression for the partition function is known, but it has both asymptotic expansions that accurately approximate it and recurrence relations by which it can be calculated exactly.[4] In both combinatorics and number theory, families of partitions subject to various restrictions are often studied.Proof (outline): The crucial observation is that every odd part can be "folded" in the middle to form a self-conjugate diagram: One can then obtain a bijection between the set of partitions with distinct odd parts and the set of self-conjugate partitions, as illustrated by the following example:If we count the partitions of 8 with distinct parts, we also obtain 6: This is a general property.[8][9] This result was proved by Leonhard Euler in 1748[10] and later was generalized as Glaisher's theorem.The first few values of q(n) are (starting with q(0)=1): The generating function for q(n) is given by[11] The pentagonal number theorem gives a recurrence for q:[12] where ak is (−1)m if k = 3m2 − m for some integer m and is 0 otherwise.By taking conjugates, the number pk(n) of partitions of n into exactly k parts is equal to the number of partitions of n in which the largest part has size k. The function pk(n) satisfies the recurrence with initial values p0(0) = 1 and pk(n) = 0 if n ≤ 0 or k ≤ 0 and n and k are not both zero.[13] One recovers the function p(n) by One possible generating function for such partitions, taking k fixed and n variable, is More generally, if T is a set of positive integers then the number of partitions of n, all of whose parts belong to T, has generating function This can be used to solve change-making problems (where the set T specifies the available coins).[14] One may also simultaneously limit the number and size of the parts.The Gaussian binomial coefficient is related to the generating function of p(N, M; n) by the equalityThis statistic (which is unrelated to the one described above) appears in the study of Ramanujan congruences.There is a natural partial order on partitions given by inclusion of Young diagrams.This partially ordered set is known as Young's lattice.The lattice was originally defined in the context of representation theory, where it is used to describe the irreducible representations of symmetric groups Sn for all n, together with their branching properties, in characteristic zero.It also has received significant study for its purely combinatorial properties; notably, it is the motivating example of a differential poset.There is a deep theory of random partitions chosen according to the uniform probability distribution on the symmetric group via the Robinson–Schensted correspondence.In 1977, Logan and Shepp, as well as Vershik and Kerov, showed that the Young diagram of a typical large partition becomes asymptotically close to the graph of a certain analytic function minimizing a certain functional.In 1988, Baik, Deift and Johansson extended these results to determine the distribution of the longest increasing subsequence of a random permutation in terms of the Tracy–Widom distribution.[17] Okounkov related these results to the combinatorics of Riemann surfaces and representation theory.
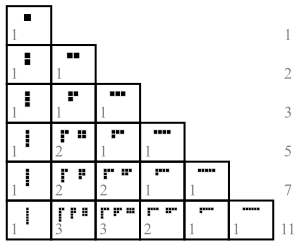

Partition of a setInfinitary combinatoricsPartition problemnumber theorycombinatoricsintegerpositive integerssummandscompositionpartition functionYoung diagramsFerrers diagramsmathematicsphysicssymmetric polynomialssymmetric groupgroup representation theoryNorman Macleod FerrersAlfred YoungYoung diagramsymmetric functionsYoung tableauxpolyominoPartition function (number theory)generating functionclosed-form expressionasymptotic expansionsrecurrence relationsexponential functionsquare rootHans Rademacherconvergent seriesDedekind summultiplicative inverseEuler functionpentagonal number theorempentagonal numberSrinivasa Ramanujanmodular arithmeticRamanujan's congruencesLeonhard EulerGlaisher's theoremTriangle of partition numberschange-making problemsGaussian binomial coefficientDurfee squareh-indexrank of a partitionRamanujan congruencesYoung's latticepartial orderrepresentation theoryirreducible representationssymmetric groupsdifferential posetRobinson–Schensted correspondenceTracy–Widom distributionOkounkovRiemann surfacesCrank of a partitionDominance orderFactorizationInteger factorizationStars and bars (combinatorics)Plane partitionPolite numberMultiplicative partitionTwelvefold wayEwens's sampling formulaFaà di Bruno's formulaMultipartitionNewton's identitiesSmallest-parts functionGoldbach's conjectureKostant's partition functionJournal of Combinatorial TheoryAndrews, George E.Abramowitz, MiltonStegun, IreneHandbook of Mathematical Functions with Formulas, Graphs, and Mathematical TablesApostol, Tom M.Graduate Texts in MathematicsSpringer-VerlagBóna, MiklósHardy, G. H.Wright, E. M.D. R. Heath-BrownJ. H. SilvermanAndrew WilesOxford University PressLehmer, D. H.Macdonald, Ian G.Rademacher, HansSautoy, Marcus Du.Stanley, Richard P.Encyclopedia of MathematicsEMS PressWeisstein, Eric W.MathWorldBrady Haran